Question

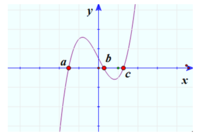
Cho hàm số y = a x 3 + b x 2 + c x + d  có đồ thị (C). Biết rằng (C) cắt trục hoành tại 3 điểm phân biệt có hoành độ x₁ > x₂ > x₃ > 0 và trung điểm nối 2 điểm cực trị của (C) có hoành độ x 0 = 1 3 .  Biết rằng 3 x 1 + 4 x 2 + 5 x 3 2 = 44 x 1 x 2 + x 2 x 3 + x 3 x 1 .  Hãy xác định tổng S = x 1 + x 2 2 + x 3 2 .  

A. 137 216 .

B. 45 157 .

C. 133 216 .

D.1

Answer 1

Chọn C.

Tập xác định: D=R Ta có y = 3 a x 2 + 2 b x + c  

Do đồ thị (C) có hai điểm cực trị nên ta có phương trình y '=0 có hai nghiệm phân biệt hay là phương trình 3 a x 2 + 2 b x + c = 0  có hai nghiệm phân biệt x_i, x_j và hai nghiệm này cũng chính là hoành độ của hai điểm cực trị của đồ thị (C). theo vi-ét ta có x i + x j = - 2 b 3 a .  

Suy ra hoành độ giao điểm nối hai điểm cực trị là

x 0 = x i + x j 2 = 1 3 ⇔ - 2 b 3 a = 2 3 ⇔ b = - a .  

Mặt khác do giả thiết ta có phương trình a x 3 + b x 2 + c x + d = 0  có ba nghiệm phân biệt x₁, x₂, x₃ nên theo vi-ét ta có   x 1 + x 2 + x 3 = - b a = a a = 1 .

Ta có:

3 x 1 + 4 x 2 + 5 x 3 2 = 44 x 1 x 2 + x 2 x 3 + x 3 x 1 ⇔ 9 x 1 2 + 16 x 2 2 + 25 x 3 2 = 20 x 1 x 2 + 4 x 2 x 3 + 14 x 3 x 1  

⇔ 20 3 x 1 2 + 40 3 x 2 2 + x 2 2 + 4 x 3 2 + 7 3 x 1 2 + 21 x 3 2 = 20 x 1 x 2 + 4 x 2 x 3 + 14 x 3 x 1  

Áp dụng bất đẳng thức Cauchuy ta có:

5 3 4 x 1 2 + 9 x 2 2 ≥ 5 3 . 2 4 x 1 1 . 9 x 2 2 = 20 x 1 x 2  (1). x 2 2 + 4 x 3 2 ≥ 2 x 2 2 . 4 x 3 2 = 4 x 1 x 2  (2). 7 12 4 x 1 2 + 36 x 3 2 ≥ 7 12 . 2 4 x 1 2 . 36 x 3 2 = 14 x 3 x 1  (3).

Lấy (1) + (2) + (3) vế theo vế ta có: 9 x 1 2 + 16 x 2 2 + 25 x 3 2 ≥ 20 x 1 x 2 + 4 x 2 x 3 + 14 x 3 x 1 .  

Dấu đẳng thức xảy ra khi và chỉ khi:

4 x 1 2 = 9 x 2 2 x 2 2 = 4 x 3 2 4 x 1 2 = 36 x 3 2 x 1 + x 2 + x 3 = 1 ⇔ x 1 = 3 2 x 2 x 2 = 2 x 3 x 3 = 1 3 x 1 x 1 + x 2 + x 3 = 1 ⇔ x 1 = 1 2 x 2 = 1 3 x 3 = 1 6 .  

Vậy S = x 1 + x 2 2 + x 3 2 = 1 2 + 1 3 2 + 1 6 3 = 133 216 .