Chọn B
Dựa vào đồ thị ta khẳng định hàm số đã cho có 2 điểm cực trị.
Chọn B
Dựa vào đồ thị ta khẳng định hàm số đã cho có 2 điểm cực trị.
Cho hàm số f x = a x 3 + b x 2 + c x + d (với a,b,c,d ϵ ℝ và a≠0) có đồ thị như hình vẽ. Số điểm cực trị của hàm số g x = f - 2 x 2 + 4 x là
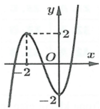
A. 2.
B. 3.
C. 4.
D. 5.
Cho hàm số f x = a x 3 + b x 2 + c x + d (với a, b, c, d ∈ ℝ và ) có đồ thị như hình vẽ. Số điểm cực trị của hàm số g x = f - 2 x 2 + 4 x là
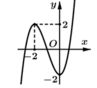
A. 2
B. 3
C. 4
D. 5
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( a , b , c ∈ ℝ , a ≠ 0 ) có đồ thị (C). Biết đồ thị (C)đi qua A(1;4) và đồ thị hàm số y ' = f x cho bởi hình vẽ.
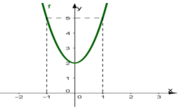
Giá trị f 3 − 2 f 1 là
A. 30
B. 27
C. 25
D. 26
Cho hàm số f x = a x + b c x + d với a , b , c , d ∈ R có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số y=f(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng.

A. 2
B. 5
C. 4
D. 6
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a,b,cÎR, a≠0) có đồ thị (C). Biết đồ thị (C) đi qua A(1;4) và đồ thị hàm số y = f ’ ( x ) cho bởi hình vẽ. Giá trị f ( 3 ) - 2 f ( 1 ) là
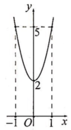
A. 30
B. 24
C. 26
D. 27
Cho hai hàm số y=f(x) và y=g(x) là hai hàm số liên tục trên ℝ có đồ thị hàm số y=f’(x) là đường cong nét đậm, đồ thị hàm số y=g’(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A, B, C của y=f’(x) và y=g’(x) trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [a;c]

A. m i n h x a ; c = h 0
B. m i n h x a ; c = h a
C. m i n h x a ; c = h b
D. m i n h x a ; c = h c
Cho hàm số y = f x = a x 3 + b x 2 + c x + d a , b , c , d ∈ ℝ , a ≠ 0 có đồ thị là C . Biết rằng đồ thị C đi qua gốc tọa độ và đồ thị hàm số y = f ' x cho bởi hình vẽ bên. Tính giá trị H = f 4 - f 2
A. H = 45
B. H = 64
C. H = 51
D. H = 58
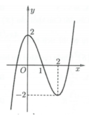
Cho hàm số f x = a x 3 + b x 2 + c x + d a , b , c , d ∈ ℝ . Đồ thị của hàm số y = f(x) như hình vẽ bên. Có bao nhiêu số nguyên m thuộc khoảng (-20;20) để phương trình 2 m - 1 f x - 3 = 0 có đúng ba nghiệm phân biệt?
A. 39
B. 38
C. 37
D. 36