Các câu hỏi tương tự
Cho hàm số
y
5
-
x
2
+
6
x
-
8
. Gọi m là giá trị thực để y’(2) 6mln5. Mệnh đề nào dưới đây đúng?
Đọc tiếp
Cho hàm số y = 5 - x 2 + 6 x - 8 . Gọi m là giá trị thực để y’(2) = 6mln5. Mệnh đề nào dưới đây đúng?
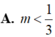
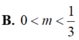
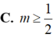
![]()
Gọi m là số thực để hàm số y= (x+ m)3 đạt giá trị lớn nhất bằng 8 trên đoạn [1; 2]. Khẳng định nào dưới đây đúng?
A. -2< m< 0
B.2< m< 4
C.-1< m< 2
D. 0 <m< 3
Cho hàm số y
(
m
-
1
)
x
3
-
3
(
m
+
2
)
x
2
-
6
(
m
+
2
)
x
+
1
. Tập giá trị của m để
y
≥
0
∀
x
∈
ℝ
là A. [3;+
∞
) B.
∅...
Đọc tiếp
Cho hàm số y = ( m - 1 ) x 3 - 3 ( m + 2 ) x 2 - 6 ( m + 2 ) x + 1 . Tập giá trị của m để y ' ≥ 0 ∀ x ∈ ℝ là
A. [3;+ ∞ )
B. ∅
C. [ 4 2 ;+ ∞ )
D. [1;+ ∞ )
Gọi A, B là hai điểm cực trị của đồ thị hàm số f(x) = x3 - 3x2 + m với m là tham số thực khác 0. Tìm tất cả các giá trị thực của tham số m để trọng tâm tam giác OAB thuộc đường thẳng 3x + 3y - 8 = 0.
A. m = 5
B. m = 2
C. m = 6
D. m = 4
Xác định giá trị của tham số m để hàm số
y = x 3 - 3(m - 1) x 2 - 3(m + 1)x - 5 có cực trị
A. m > 0 B. -1 < m < 1
C. m ≤ 0 D. ∀m ∈ R.
Xác định giá trị của tham số m để hàm số
y = x 3 - 3(m - 1) x 2 - 3(m + 1)x - 5 có cực trị
A. m > 0 B. -1 < m < 1
C. m ≤ 0 D. ∀ m ∈ R.
Xác định giá trị của tham số m để hàm số sau không có cực trị
y = m x 3 /3 + m x 2 + 2(m - 1)x - 2.
A. m ≤ 0 hoặc m ≥ 2 B. m ≥ 0
C. m ≤ 0 ≤ 2 D. m ∈ [0; + ∞ ]
Xác định giá trị của tham số m để hàm số sau không có cực trịy m
x
3
/3 + m
x
2
+ 2(m - 1)x - 2.A. m
≤
0 hoặc m
≥
2 B. m
≥
0C. m
≤
0
≤
2 D. m ∈ [0; +
∞
]
Đọc tiếp
Xác định giá trị của tham số m để hàm số sau không có cực trị
y = m x 3 /3 + m x 2 + 2(m - 1)x - 2.
A. m ≤ 0 hoặc m ≥ 2 B. m ≥ 0
C. m ≤ 0 ≤ 2 D. m ∈ [0; + ∞ ]
Gọi M là giá trị lớn nhất của hàm số y
x
3
-
3
x
2
+
x
+
m
xét trên đoạn [2;4], m0 là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng. A. 1
m
0
5 B. -7
m...
Đọc tiếp
Gọi M là giá trị lớn nhất của hàm số y = x 3 - 3 x 2 + x + m xét trên đoạn [2;4], m0 là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng.
A. 1 < m 0 < 5
B. -7 < m 0 < -5
C. -4 < m 0 < 0
D. m 0 < -8