Ta có đạo hàm y’ = 3( x+ m) 2≥0 với mọi x.
=> Hàm số đồng biến trên đoạn [1; 2] nên hàm số đạt GTLN tại x = 2.
Khi đó; y( 2) = 8 khi và chỉ khi : ( 2+m) 3 = 8 hay m= 0
Chọn C.
Ta có đạo hàm y’ = 3( x+ m) 2≥0 với mọi x.
=> Hàm số đồng biến trên đoạn [1; 2] nên hàm số đạt GTLN tại x = 2.
Khi đó; y( 2) = 8 khi và chỉ khi : ( 2+m) 3 = 8 hay m= 0
Chọn C.
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x + m x + 1 trên [1;2] bằng 8 (m là tham số thực). Khẳng định nào sau đây đúng?
A. m > 10
B. 8 < m < 10
C. 0 < m < 4
D. 4 < m < 8
Gọi M là giá trị lớn nhất của hàm số y = x 3 - 3 x 2 + x + m xét trên đoạn [2;4], m0 là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng.
A. 1 < m 0 < 5
B. -7 < m 0 < -5
C. -4 < m 0 < 0
D. m 0 < -8
Cho hàm số y = f(x) có đồ thị hàm số như hình vẽ dưới. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f( x 2 - 2 x ) trên đoạn [ - 3 2 ; 7 2 ] Tìm khẳng định đúng trong các khẳng định sau
A. ![]()
B.![]()
C.![]()
D.![]()
Biết phương trình log 5 2 x + 1 x = 2 log 3 ( x 2 - 1 2 x ) có nghiệm duy nhất x = a + b 2 trong đó a, b là các số nguyên. Hỏi m thuộc khoảng nào dưới đây để hàm số y = m x + a - 2 x - m có giá trị lớn nhất trên đoạn [1; 2] bằng -2
A. m ∈ ( 2 ; 4 )
B. m ∈ ( 4 ; 6 )
C. m ∈ ( 6 ; 7 )
D. m ∈ ( 7 ; 9 )
Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số y = x 2 - 3 x + m trên đoạn [ 0; 2] bằng 3. Số phần tử của S là
A. 1
B. 2
C. 3
D. 5
Cho các số thực x 1 , x 2 , x 3 , x 4 thỏa mãn 0 < x 1 < x 2 < x 3 < x 4 và hàm số y=f(x). Biết hàm số y=f’(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 0 ; x 4 . Đáp áp nào sau đây đúng?
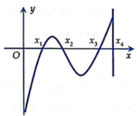
A. M + m = f 0 + f x 3 .
B. M + m = f x 3 + f x 4 .
C. M + m = f x 1 + f x 2 .
D. M + m = f 0 + f x 1 .
Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất củ hàm số y = 3sinx - 4cosx + 1. Khẳng định nào sau đây là đúng?
A. M = 4; m = -6
B. M = 6; m = -4
C. M = 3; m = -4
D. M = 5; m = -5
Xác định giá trị của tham số m để hàm số sau không có cực trị
y = m x 3 /3 + m x 2 + 2(m - 1)x - 2.
A. m ≤ 0 hoặc m ≥ 2 B. m ≥ 0
C. m ≤ 0 ≤ 2 D. m ∈ [0; + ∞ ]
Xác định giá trị của tham số m để hàm số sau không có cực trị
y = m x 3 /3 + m x 2 + 2(m - 1)x - 2.
A. m ≤ 0 hoặc m ≥ 2 B. m ≥ 0
C. m ≤ 0 ≤ 2 D. m ∈ [0; + ∞ ]