Chọn B.
Ta có 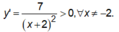
Do đó hàm số đồng biến trên [0;2].
Suy ra 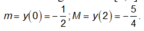
Do đó 4M – 2m = 6.
Chọn B.
Ta có 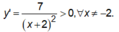
Do đó hàm số đồng biến trên [0;2].
Suy ra 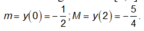
Do đó 4M – 2m = 6.
Cho hàm số y = f(x) = | x 4 - 4 x 3 + 4 x 2 + a |. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn [0;2]. Số giá trị nguyên a thuộc đoạn [-3;3] sao cho M ≤ 2m là
A. 3
B. 5
C. 6
D. 7
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 3 - 3 x + 2 trên đoạn [0;2]. Khi đó tổng M+m bằng.
A. 4
B. 12
C. 2
D. 6
Cho hàm số f(x) = | x 4 - 4 x 3 + 4 x 2 + a |. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [0;2]. Có bao nhiêu số nguyên a thuộc đoạn [-3;2] sao cho M ≤ 2m?
A. 7
B. 5
C. 6
D. 4
Cho hàm số y = 3 x - 1 x - 3 . Gọi giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [0;2] lần lượt là M và m. Khi đó S=m+M có giá trị là
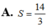
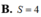
![]()
![]()
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x)= x^3-3x^2+2 trên đoạn [-1,2] . Tính giá trị biểu thức P= M-2m A. 3√2-3 B. 2√2-5 C. 3√3-5 D. 3√3-3
Cho hàm số y = 2 - x 2 Gọi M và n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Khi đó
M - 2m bằng
A. 2 2
B. 0
C. - 2
D. 2
Cho hàm số y = f (x) liên tục trên đoạn [−2;6] có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của f (x) trên đoạn [−2;6]. Giá trị của 2M +3m bằng
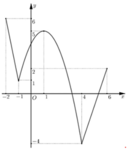
A. 16
B. 0
C. 7
D. 2
Cho hàm số y = f x , x ∈ - 2 ; 3 có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn - 2 ; 3 . Giá trị của biểu thức 2 m + log 9 M bằng?
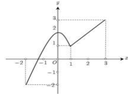
A. 1 8
B. 3 8
C. 3 4
D. 3 2
Cho hàm số y = x 4 - 4 x 3 + 4 x 2 + a . Gọi M; m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [0; 2] . Có bao nhiêu số nguyên a thuộc đoạn [ -3; 3] sao cho M≤ 2m?
A. 4
B. 5
C. 6
D. 3