Đáp án C.
TXĐ: D = R.
Ta có y’ = 6x2 + 6x - 12, y’ = 0 ó 6x2 + 6x – 12 = 0 ó x = 1 hoặc x = -2.
y’’ = 12x + 12, y’’(1) = 24 > 0 => x2 = 1 là điểm cực tiểu, y’’(-2) = -12 < 0 => x1 - 2 là điểm cực đại.
Vậy ta có x2 – x1 = 3.
Cho hàm số y = 2 x 3 + 3 x 2 - 12 x + 2019 . Gọi x 1 và x 2 lần lượt là điểm cực đại và cực tiểu của hàm số. Kết luận nào sau đây là đúng
Cho hàm số y = x 3 - 6 x 2 + 4 x - 7 . Gọi hoành độ 2 điểm cực trị của đồ thị hàm số là x 1 , x 2 . Khi đó, giá trị của tổng x 1 + x 2 là
A. -6
B. -4
C. 6
D. 4
Cho hàm số y = f ( x ) = ax 3 + bx 2 + cx + d có hai cực trị x 1 , x 2 thỏa - 2 < x 1 < 0 < x 2 < 2 và có đồ thị như hình vẽ.
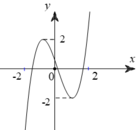
Số điểm cực tiểu của hàm số 
là
A. 3.
B. 5.
C. 7.
D. 4.
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 3 x 3 - m x 2 - 2 ( 3 m 2 - 1 ) x + 2 3 có hai điểm cực trị có hoành độ x 1 , x 2 sao cho x 1 x 2 + 2 ( x 1 + x 2 ) = 1
A. m = 0
B. m = - 2 3
C. m = 2 3
D. m = - 1 2
Gọi x 1 , x 2 là hai điểm cực trị của hàm số f(x) = 1 3 x 3 - 3 x 2 - 2 x . Giá trị của x 1 2 + x 2 2 bằng:
A. 13
B. 32
C. 4
D. 36
Gọi x 1 , x 2 là hai điểm cực trị của hàm số y = x 3 - 3 m x 2 + 3 ( m 2 - 1 ) x - m 3 + m . Tìm tất cả các giá trị của tham số thực m để : x 1 2 + x 2 2 - x 1 x 2 = 7
A. m = ± 2 .
B. m = ± 2 .
C. m = 0 .
D. m = ± 1 .
Giả sử đồ thị (C) của hàm số f x = a x 3 + b x 2 + c x + d có hai điểm cực trị là M ( - 1 ; 7 ) và N ( 5 ; - 7 ) . Gọi x 1 ; x 2 ; x 3 là hoành độ giao điểm của (C) với trục hoành. Khi đó x 1 + x 2 + x 3 bằng
A. 6
B. 4
C. 3
D. 2
Giá trị của tham số m để hàm số y = x 3 - 3 x 2 + m x - 1 có hai cực trị x 1 , x 2 thỏa mãn x 1 2 + x 2 2 = 6 là
A. 1.
B. -1.
C. 3.
D. -3.
Cho hàm số y = x 3 - 3 x 2 + m x - 1 với m là tham số thực. Tìm tất cả các giá trị của tham số m để hàm số đạt cực trị tại hai điểm x 1 , x 2 thỏa x 1 2 + x 2 2 = 6 .
A. 3.
B. -1.
C. 1.
D. -3.
