Đáp án C.
Ta có 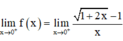
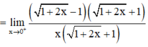
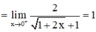
Mặt khác ![]()
Hàm số liên tục tại điểm x = 0
![]()
![]()
Đáp án C.
Ta có 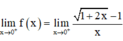
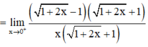
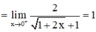
Mặt khác ![]()
Hàm số liên tục tại điểm x = 0
![]()
![]()
Cho hàm số f x = 3 x + a - 1 k h i x ≤ 0 1 + 2 x - 1 x k h i x > 0 . Tìm tất cả giá trị của a để hàm số đã cho liên tục tại điểm x = 0
A. a = 1
B. a = 3
C. a = 2
D. a = 4
Cho hàm số f x = 3 x + a - 1 k h i x ≤ 0 1 + 2 x - 1 x k h i x > 0 . Tìm tất cả giá trị của a để hàm số đã cho liên tục tại điểm x = 0.
A. a = 1
B. a = 3
C. a = 2
D. a = 4
Cho hàm số f ( x ) = 3 x + a - 1 k h i x ≤ 0 1 + 2 x - 1 x k h i x > 0 . Tìm tất cả giá trị của a để hàm số đã cho liên tục tại điểm x = 0
A. a = 1.
B. a = 3.
C. a = 2.
D. a = 4.
Cho hàm số f x = 3 x + a − 1 k h i x ≤ 0 1 + 2 x − 1 k h i x > 0 x . Tìm tất cả giá trị của a để hàm số đã cho liên tục trên i
A. a=1
B. a=3
C. a=2
D. a=4
Cho hàm số y = f x = e a x − e 3 x 2 x khi x ≠ 0 1 2 khi x = 0 . Tìm giá trị của a để hàm số f(x) liên tục tại điểm x=0
A. a = 2
B. a = 4
C. a = − 1 4
D. a = − 1 2
Cho hàm số y = f x = e a x - e 3 x 2 x k h i x ≠ 0 1 2 k h i x = 0 . Tìm giá trị của a để hàm số f(x) liên tục tại điểm x = 0.
A. a = 2
B. a = 4
C. a = - 1 4
D. a = - 1 2
Cho các mệnh đề :
1) Hàm số y=f(x) có đạo hàm tại điểm x 0 thì nó liến tục tại x 0 .
2) Hàm số y=f(x) liên tục tại x 0 thì nó có đạo hàm tại điểm x 0 .
3) Hàm số y=f(x) liên tục trên đoạn [a;b] và f(a).f(b)<0 thì phương trình f(x) có ít nhất một nghiệm trên khoảng (a;b).
4) Hàm số y=f(x) xác định trên đoạn [a;b] thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
Số mệnh đề đúng là:
A. 2
B. 4
C. 3
D. 1
Cho hàm số f x = x 2 + 4 − 2 x 2 k h i x ≠ 0 2 a − 5 4 khi x = 0 . Tìm giá trị thực của tham số a để hàm số f(x) liên tục tại x = 0
A. a = - 3 4
B. a = 4 3
C. a = - 4 3
D. a = 3 4
Cho các mệnh đề sau:
1. Nếu hàm số y = f x liên tục, có đạo hàm tới cấp hai trên a ; b , x 0 ∈ a ; b và f ' x 0 = 0 f ' ' x 0 ≠ 0 thì x0 là một điểm cực trị của hàm số.
2. Nếu hàm số y = f x xác định trên a ; b thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
3. Nếu hàm số y = f x liên tục trên a ; b thì hàm số có đạo hàm tại mọi x thuộc [a;b].
4. Nếu hàm số y = f x có đạo hàm trên a ; b thì hàm số có nguyên hàm trên a ; b
Số mệnh đề đúng là:
A. 2
B. 1
C. 3
D. 4