Các câu hỏi tương tự
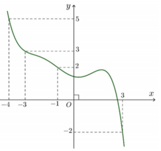
Cho hàm số f(x). Biết hàm số yf (x) có đồ thị như hình bên. Trên đoạn [-4;3], hàm số
g
(
x
)
2
f
(
x
)
+
(
1
-
x
)
2
đạt giá trị nhỏ nhất tại điểm A.. B.. C.. D....
Đọc tiếp
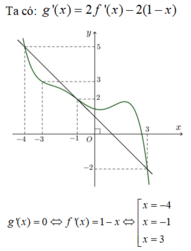
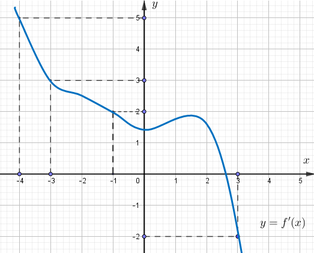
Cho hàm số f(x). Biết hàm số y=f '(x) có đồ thị như hình bên. Trên đoạn [-4;3], hàm số g ( x ) = 2 f ( x ) + ( 1 - x ) 2 đạt giá trị nhỏ nhất tại điểm
A.
.
B.
.
C.
.
D.
.
Cho hàm số f(x). Biết hàm số y f(x) có đồ thị như hình bên. Trên đoạn [-4;3], hàm số g(x) 2f(x) +
1
-
x
2
đạt giá trị nhỏ nhất tại điểm A.
x
0
-4 B.
x
0
-1 C.
x
0
3 D.
x
0
-3
Đọc tiếp
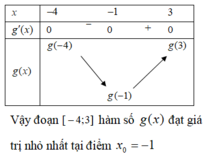
Cho hàm số f(x). Biết hàm số y = f'(x) có đồ thị như hình bên. Trên đoạn [-4;3], hàm số g(x) = 2f(x) + 1 - x 2 đạt giá trị nhỏ nhất tại điểm
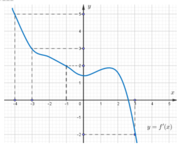
A. x 0 = -4
B. x 0 = -1
C. x 0 = 3
D. x 0 = -3
Cho hàm số f(x) có đạo hàm là hàm f(x). Đồ thị hàm số f(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4]. A. m f(4), M f(2) B. m f(1), M f(2) C. m f(4), M f(1) D. m f(0), M f(2)
Đọc tiếp
Cho hàm số f(x) có đạo hàm là hàm f'(x). Đồ thị hàm số f'(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) = f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4].
A. m = f(4), M = f(2)
B. m = f(1), M = f(2)
C. m = f(4), M = f(1)
D. m = f(0), M = f(2)
Cho hàm số f(x) có đạo hàm là f(x). Đồ thị của hàm số y f(x) được cho như hình vẽ dưới đây: Biết rằng f(-1) + f(0) f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y f(x) trên đoạn [-1;2] lần lượt là: A. f(1);f(2) B. f(2);f(0) C. f(0);f(2) D. f(1);f(-1)
Đọc tiếp
Cho hàm số f(x) có đạo hàm là f'(x). Đồ thị của hàm số y = f'(x) được cho như hình vẽ dưới đây:
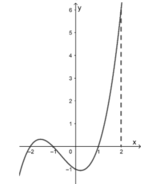
Biết rằng f(-1) + f(0) < f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f(x) trên đoạn [-1;2] lần lượt là:
A. f(1);f(2)
B. f(2);f(0)
C. f(0);f(2)
D. f(1);f(-1)
Cho hàm số y f(x) xác định trên tập số thực và có đạo hàm f(x). Đồ thị hàm số y f(x) được cho bởi hình bên dưới. Biết rằng f(0) + f(1) - 2f(2) f(4). - f(3). Giá trị nhỏ nhất của hàm số y f(x) trên đoạn [0;4] là A. f(1) B. f(0) C. f(2) D. f(4)
Đọc tiếp
Cho hàm số y = f(x) xác định trên tập số thực và có đạo hàm f'(x). Đồ thị hàm số y = f'(x) được cho bởi hình bên dưới. Biết rằng f(0) + f(1) - 2f(2) = f(4). - f(3). Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [0;4] là
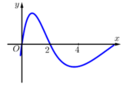
A. f(1)
B. f(0)
C. f(2)
D. f(4)
Cho hàm số f(x) có đồ thị của hàm số f(x) như hình vẽ. Biết f(0) + f(1) - 2f(2) f(4) - f(3). Giá trị nhỏ nhất m, giá trị lớn nhất M của hàm số f(x) trên đoạn [0;4] là A. m f(4), M f(1) B. m f(4), M f(2) C. m f(1), M f(2) D. m f(0), M f(2)
Đọc tiếp
Cho hàm số f(x) có đồ thị của hàm số f'(x) như hình vẽ. Biết f(0) + f(1) - 2f(2) = f(4) - f(3). Giá trị nhỏ nhất m, giá trị lớn nhất M của hàm số f(x) trên đoạn [0;4] là
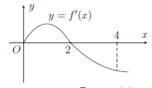
A. m = f(4), M = f(1)
B. m = f(4), M = f(2)
C. m = f(1), M = f(2)
D. m = f(0), M = f(2)
Cho hàm số f(x) có đạo hàm cấp hai f(x) liên tục trên R và có đồ thị hàm số f(x) như hình vẽ bên. Biết rằng hàm số f(x) đạt cực đại tại điểm x 1 đường thẳng trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x 2 . Tích phân
∫
0
ln
3
e
x
f
e...
Đọc tiếp
Cho hàm số f(x) có đạo hàm cấp hai f''(x) liên tục trên R và có đồ thị hàm số f(x) như hình vẽ bên. Biết rằng hàm số f(x) đạt cực đại tại điểm x = 1 đường thẳng 
trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 . Tích phân
∫
0
ln
3
e
x
f
"
e
x
+
1
2
d
x
bằng
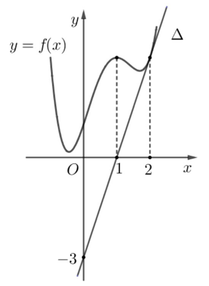
A. 8
B. 4
C. 3
D. 6
Cho hàm số f(x) có đạo hàm cấp hai f(x) liên tục trên R và đồ thị hàm số f(x) như hình vẽ bên. Biết rằng hàm số f(x) đạt cực đại tại điểm x1; đường thẳng
∆
trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x2. Tích phân
∫
0
ln
3
e
x
f
(
e
x...
Đọc tiếp
Cho hàm số f(x) có đạo hàm cấp hai f'''(x) liên tục trên R và đồ thị hàm số f(x) như hình vẽ bên. Biết rằng hàm số f(x) đạt cực đại tại điểm x=1; đường thẳng ∆ trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x=2. Tích phân ∫ 0 ln 3 e x f ' ' ( e x + 1 2 ) d x bằng
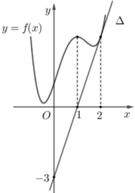
A. 8
B. 4
C. 3
D. 6
Cho hàm số y= f( x) có đạo hàm trên R. Đồ thị hàm số y= f’(x) như hình vẽ bên dưới. Hàm số g(x) = 2f(x) + x2 đạt cực tiểu tại điểm
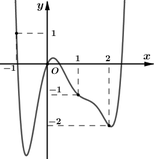
A . x=-1
B. x= 0
C . x= 1
D.x= 2