Các câu hỏi tương tự
Cho hàm số
f
(
x
)
x
4
-
4
x
2
+
1
Khi đó, phương trình
f
(
f
(
f
(
x
)
-
1
)
-
2
)
1
có bao nhiêu nghiệm thực phân biệt A. 24 B. 22 C. 26 D. 32
Đọc tiếp
Cho hàm số f ( x ) = x 4 - 4 x 2 + 1 Khi đó, phương trình f ( f ( f ( x ) - 1 ) - 2 ) = 1 có bao nhiêu nghiệm thực phân biệt
A. 24
B. 22
C. 26
D. 32
Cho hàm số y f(x) xác định trên
ℝ
. Đồ thị hàm số y f (x) cắt trục hoành tại ba điểm có hoành độ
a
,
b
,
c
a
b
c
như hình vẽ. Biết f (b)0, hỏi phương trình f(x) 0 có nhiều nhất bao nhiêu nghiệm? A. 1. B. 2. C. 3. D. 4.
Đọc tiếp
Cho hàm số y = f(x) xác định trên ℝ . Đồ thị hàm số y = f '(x) cắt trục hoành tại ba điểm có hoành độ a , b , c a < b < c như hình vẽ. Biết f (b)<0, hỏi phương trình f(x) = 0 có nhiều nhất bao nhiêu nghiệm?
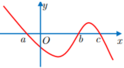
A. 1.
B. 2.
C. 3.
D. 4.
Cho hàm số
f
(
x
)
1
3
x
3
-
x
2
+
x
+
3
-
log
3
m
Có bao nhiêu số nguyên m để phương trình
f
(
f
(
f
(
f
(
x
)
)
)
)
x
có 3...
Đọc tiếp
Cho hàm số f ( x ) = 1 3 x 3 - x 2 + x + 3 - log 3 m Có bao nhiêu số nguyên m để phương trình f ( f ( f ( f ( x ) ) ) ) = x có 3 nghiệm thực phân biệt
A. 20
B. 18
C. 19
D. 17
Cho các mệnh đề:1. Nếu hàm số yf(x) liên tục trên
a
;
b
và
f
a
.
f
b
0
thì tồn tại
x
0
∈
a
;
b
sao cho
f
x
0
0.
2. Nếu hàm số...
Đọc tiếp
Cho các mệnh đề:
1. Nếu hàm số y=f(x) liên tục trên a ; b và f a . f b < 0 thì tồn tại x 0 ∈ a ; b sao cho f x 0 = 0.
2. Nếu hàm số y = f x liên tục trên a ; b và f a . f b < 0 thì phương trình f x = 0 có nghiệm.
3. Nếu hàm số y=f(x) liên tục, đơn điệu trên a ; b và f a . f b < 0 thì phương trình f x = 0 có nghiệm duy nhất trên ( a ; b ) .
Trong ba mệnh đề trên
A. Có đúng hai mệnh đề sai
B. Cả ba mệnh đề đều đúng
C. Cả ba mệnh đề đều sai
D. Có đúng một mệnh đề sai
Cho số thực m và hàm số yf(x) có đồ thị như hình vẽ. Phương trình
f
(
2
x
+
2
-
x
)
m
nhiều nhất bao nhiêu nghiệm phân biệt thuộc đoạn [-1;2]? A. 2 B. 3 C. 4 D. 5
Đọc tiếp
Cho số thực m và hàm số y=f(x) có đồ thị như hình vẽ. Phương trình f ( 2 x + 2 - x ) = m nhiều nhất bao nhiêu nghiệm phân biệt thuộc đoạn [-1;2]?

A. 2
B. 3
C. 4
D. 5
Cho hàm số yf(x) có đồ thị trong hình bên. Phương trình f(x)1 có bao nhiêu nghiệm thực phân biệt nhỏ hơn 2? A. 1. B. 2. C. 3. D. 0.
Đọc tiếp
Cho hàm số y=f(x) có đồ thị trong hình bên. Phương trình f(x)=1 có bao nhiêu nghiệm thực phân biệt nhỏ hơn 2?

A. 1.
B. 2.
C. 3.
D. 0.
Cho hàm số
y
f
(
x
)
liên tục trên
ℝ
và có đồ thị như hình vẽ bên. Xét 4 mệnh đề sau(1) Hàm số
y
f
(
x
)
đạt cực đại tại
x
0
0
(2) Hàm số
y
f
(
x
)
có ba cực trị.(3) Phương trình
y
f
(
x
)
có đúng ba nghiệm phân biệt(4) Hàm...
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên ℝ và có đồ thị như hình vẽ bên. Xét 4 mệnh đề sau
(1) Hàm số y = f ( x ) đạt cực đại tại x 0 = 0
(2) Hàm số y = f ( x ) có ba cực trị.
(3) Phương trình y = f ( x ) có đúng ba nghiệm phân biệt
(4) Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]
Hỏi trong 4 mệnh đề trên, có bao nhiêu mệnh đề đúng?

A. 1
B. 3
C. 4
D. 2
Cho hàm số
f
x
a
x
3
+
b
x
2
+
c
x
+
d
a
,
b
,
c
,
d
∈
R
có đồ thị như hình vẽ bên.Phương trình f(f(f(f(x))))0 có tất cả bao nhiêu nghiệm thực ph...
Đọc tiếp
Cho hàm số f x = a x 3 + b x 2 + c x + d a , b , c , d ∈ R có đồ thị như hình vẽ bên.
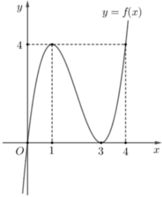
Phương trình f(f(f(f(x))))=0 có tất cả bao nhiêu nghiệm thực phân biệt?
A. 12
B. 40
C. 41
D. 16
Cho hàm số f(x) có đạo hàm
f
x
x
3
-
3
x
x
2
-
3
x
, với mọi
x
∈
R
. Phương trình f(x)0 có tối đa bao nhiêu nghiệm thực phân biệt. A. 6 B. 4 C. 5 D. 3
Đọc tiếp
Cho hàm số f(x) có đạo hàm f ' x = x 3 - 3 x x 2 - 3 x , với mọi x ∈ R . Phương trình f(x)=0 có tối đa bao nhiêu nghiệm thực phân biệt.
A. 6
B. 4
C. 5
D. 3