Đáp án C.
- Phương pháp:
+) Tính f'(x).
+) Sử dụng quy tắc trong trái ngoài cùng giải bất phương trình bậc hai.
- Cách giải:
+ Ta có:
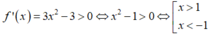
→ Vậy tập nghiệm của bất phương trình là 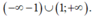
Đáp án C.
- Phương pháp:
+) Tính f'(x).
+) Sử dụng quy tắc trong trái ngoài cùng giải bất phương trình bậc hai.
- Cách giải:
+ Ta có:
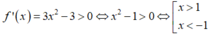
→ Vậy tập nghiệm của bất phương trình là 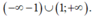
Cho hàm số f ( x ) = 1 - 3 x + x 2 x - 1 . Tập nghiệm của bất phương trình f'(x) > 0 là:
A. R\{1}
B. ∅
C. 1 ; + ∞
D. R
Cho hàm số f(x) = 5(x + 1)3 + 4(x + 1). Tập nghiệm của phương trình f ”(x) = 0 là
A. [-1 ; 2] .
B. -1.
C. {-1}.
D. ∅.
Cho hàm số f ( x ) = 5 ( x + 1 ) 3 + 4 ( x + 1 ) . Tập nghiệm của phương trình f ' ' ( x ) = 0 là
A. [-1;2]
B. ( - ∞ ; 0 ]
C. {1}
D. ∅
1) cho hàm số \(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}x^2+8x-1\) có đạo hàm là f'(x). Tập hợp những giá trị của x để f'(x) = 0
2) cho hàm số \(f\left(x\right)=\dfrac{3-3x+x^2}{x-1}\) giải bất phương trình f'(x) = 0
Cho hàm số f ( x ) = 1 3 x 3 - x 2 + 2 x - 2009 . Tập nghiệm của bất phương trình f'(x) ≤ 0 là:
A. ∅
B. [-2;2]
C. 0 ; + ∞
D. R
Cho hàm số 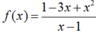 . Tập nghiệm của bất phương trình f’(x) > 0 là
. Tập nghiệm của bất phương trình f’(x) > 0 là
A. R \ {1}.
B. ∅.
C. (1; +∞).
D. R.
Cho hàm số f ( x ) = 2 m x - m x 3 . Số x = 1 là nghiệm của bất phương trình f'(x) ≤ 1 khi và chỉ khi:
A. m ≥ 1
B. m ≥ - 1
C. - 1 ≤ m ≤ 1
D. m ≥ - 1
Cho hàm số f ( x ) = 2 m x - m x 3 . Số x = 1 là nghiệm của bất phương trình f'(x) ≤ 1 khi và chỉ khi
A. m ≥ 1
B. m ≤ - 1
C. - 1 ≤ m ≤ 1
D. m ≥ - 1
Cho hàm số f ( x ) = 2 m x - m x 3 . Số x=1 là nghiệm của bất phương trình f'(x)≤1 khi và chỉ khi:
A. m≤-1
B. m≥-1
C. -1≤m≤1
D. m≥-1