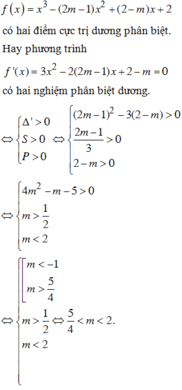Question

Cho hàm số f x = x 3 - 2 x - 1 x 2 + 2 - m x + 2 . Tìm tất cá các giá trị thực của tham số m để hàm số y = f x  có 5 cực trị.

A.  - 2 < m < 5 4

B.  - 5 4 < m < 2

C.  5 4 ≤ m ≤ 2

D.  5 4 < m < 2

Answer 1

Chọn D.

Phương pháp:

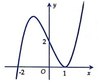
Sử dụng tính chất đồ thị hàm đa thức bậc ba luôn cắt trục tung và đồ hàm số y=f(|x|)  luôn nhận trục tung làm trục đối xứng để suy ra x=0 luôn là một cực trị của hàm y=f(|x|)   

Lập luận để suy ra hàm f(x) có hai điểm cực trị dương phân biệt thì hàm số y=f(|x|) có 5 điểm cực trị

phân biệt.

Cách giải:

Nhận thấy rằng nếu x 0  là điểm cực trị của hàm số y=f(|x|) cũng là điểm cực trị của hàm số y=f(|x|) (1)

Lại thấy vì đồ thị hàm số y=f(|x|) nhận trục Oy làm trục đối xứng mà f(x) là hàm đa thứ bậc ba nên x=0 luôn là một điểm cực trị của hàm số y=f(|x|) (2)

Từ (1) và (2) suy ra để hàm số y=f(|x|) có 5 điểm cực trị thì hàm số