Chọn A
Ta có:
Lấy nguyên hàm hai vế theo x ta được
Mà f 1 = 3 nên ta có C = 0
Từ đó x f x = 2 x 2 + x
⇒ f x = 2 x + 1 ( d o x > 0 )
Suy ra f 2 = 5
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho F(x) là một nguyên hàm của hàm số f(x)|1+x|-|1-x| trên tập R và thỏa mãn F(1) 3.Tính tổng F(0)+F(2)+F(-3).
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số f(x)=|1+x|-|1-x| trên tập R và thỏa mãn F(1)= 3.Tính tổng F(0)+F(2)+F(-3).
Cho F(x) là một nguyên hàm của hàm số f(x) = |1+x| - |1-x| trên tập R và thỏa mãn F(1) = 3 Tính tổng T = F(0) + F(2) + F(-3)
A. 8.
B. 12.
C. 18.
D. 10.
Cho hàm số f(x) thỏa mãn f(x)f(x)1 với mọi x
∈
R. Biết
∫
1
2
f
(
x
)
d
x
a
và f(1)b, f(2)c Tích phân
∫
1
2
x
f
(
x
)
d
x
bằng
Đọc tiếp
Cho hàm số f(x) thỏa mãn f(x)f'(x)=1 với mọi
x ∈ R. Biết ∫ 1 2 f ( x ) d x = a và f(1)=b, f(2)=c Tích phân ∫ 1 2 x f ( x ) d x bằng
Cho hàm số f(x) xác định trên
ℝ
-
2
;
1
thỏa mãn
f
(
x
)
1
x
2
+
x
-
2
;
f
(
0
)
...
Đọc tiếp
Cho hàm số f(x) xác định trên ℝ \ - 2 ; 1 thỏa mãn f ' ( x ) = 1 x 2 + x - 2 ; f ( 0 ) = 1 3 và f(3)-f(-3) = 0 Tính giá trị của biểu thức T = f(-4)+f(-1)-f(4)
Cho F(x) là một nguyên hàm của hàm số
f
(
x
)
1
x
-
1
thỏa mãn F(5)2 và F(0)1. Tính F(2)-F(-1).
Đọc tiếp
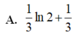
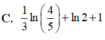
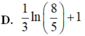
Cho F(x) là một nguyên hàm của hàm số f ( x ) = 1 x - 1 thỏa mãn F(5)=2 và F(0)=1. Tính F(2)-F(-1).
Cho hàm số f(x) có đạo hàm trên
ℝ
thỏa mãn f’(x) – 2018f(x) 2018.x2017.e2018x với mọi
x
∈
ℝ
và f(0) 2018. Tính giá trị f(1). A. f(1) 2019e2018. B. f(1) 2018e-2018. C. f(1) 2018e2018. D. f(1) 2017e2018.
Đọc tiếp
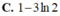
Cho hàm số f(x) có đạo hàm trên ℝ thỏa mãn f’(x) – 2018f(x) = 2018.x2017.e2018x với mọi x ∈ ℝ và f(0) = 2018. Tính giá trị f(1).
A. f(1) = 2019e2018.
B. f(1) = 2018e-2018.
C. f(1) = 2018e2018.
D. f(1) = 2017e2018.
Cho hàm số f(x) thỏa mãn
f
x
.
f
x
1
, với mọi
x
∈
R
. Biết
∫
1
2
f
x
d
x...
Đọc tiếp
Cho hàm số f(x) thỏa mãn f x . f ' x = 1 , với mọi x ∈ R . Biết ∫ 1 2 f x d x = a và f(1) = b, f(2) = c. Tích phân ∫ 1 2 x f x d x bằng
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số f(x) có đạo hàm trên R thỏa mãn f(x)-2018f(x)
2018
x
2017
e
2018
x
với mọi
x
∈
ℝ
, f(0)2018. Tính f(1)
Đọc tiếp
Cho hàm số f(x) có đạo hàm trên R thỏa mãn f'(x)-2018f(x)= 2018 x 2017 e 2018 x với mọi x ∈ ℝ , f(0)=2018. Tính f(1)
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Cho hàm số f(x) thỏa mãn các điều kiện f(1) 2,
f
x
≠
0
∀
x
0
và
x
2
+
1
2
f...
Đọc tiếp
Cho hàm số f(x) thỏa mãn các điều kiện f(1) = 2, f x ≠ 0 ∀ x > 0 và x 2 + 1 2 f ' x = f x 2 x 2 - 1 với mọi x>0. Giá trị của f(2) bằng
A. 
.
B. 
.
C. 
.
D. 
.