Các câu hỏi tương tự
Cho hàm số yf(x) liên tục và có đạo hàm tới cấp hai trên a,b ;
x
0
∈
a
;
b
. Chọn khẳng định đúng trong các khẳng định sau: A. Nếu
f
x
0
0...
Đọc tiếp
Cho hàm số y=f(x) liên tục và có đạo hàm tới cấp hai trên a,b ; x 0 ∈ a ; b . Chọn khẳng định đúng trong các khẳng định sau:
A. Nếu f ' x 0 = 0 f ' ' x 0 < 0 thì x 0 là một điểm cực tiểu của hàm số
B. Nếu f ' x 0 = 0 f ' ' x 0 ≠ 0 thì x 0 là một điểm cực trị của hàm số.
C. Nếu f ' x 0 = 0 f ' ' x 0 > 0 thì x 0 là một điểm cực đại của hàm số
D. A, B, C đều sai.
Cho hàm số yf(x) liên tục trên R và có đạo hàm
f
’
(
x
)
(
x
+
2
)
(
x
-
1
)
2018
(
x
-
2
)
2019
. Khẳng định nào sau đây là đúng? A. Hàm số có ba điểm cực trị B. Hàm số nghịch biến trên khoảng (-2;2) C. Hàm số đạt cực đại tại điểm
x...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đạo hàm f ’ ( x ) = ( x + 2 ) ( x - 1 ) 2018 ( x - 2 ) 2019 . Khẳng định nào sau đây là đúng?
A. Hàm số có ba điểm cực trị
B. Hàm số nghịch biến trên khoảng (-2;2)
C. Hàm số đạt cực đại tại điểm x = 1 và đạt cực tiểu tại các điểm x = ± 2
D. Hàm số đồng biến trên mỗi khoảng (1;2) và (2;+∞)
Cho hàm số y f(x) có đạo hàm f(x) liên tục trên R và đồ thị của hàm số f(x) trên đoạn [ -2;6] như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau. A.
maxf
x
−
2
;
6
f
−
1
B.
maxf
x...
Đọc tiếp
Cho hàm số y= f(x) có đạo hàm f'(x) liên tục trên R và đồ thị của hàm số f'(x) trên đoạn [ -2;6] như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau.
A. maxf x − 2 ; 6 = f − 1
B. maxf x − 2 ; 6 = f − 2
C. maxf x − 2 ; 6 = f 6
D. maxf x − 2 ; 6 = m ax f − 1 , f 6
Cho hàm số f(x) liên tục trên R và có bảng xét dấu đạo hàm dưới đây:Khẳng định nào sau đây đúng? A. Hàm số nghịch biến trên khoảng
−
∞
;
−
3
B. Hàm số đồng biến trên khoảng
0
;
3
C. Hàm số đồng biến trên khoảng
3
;...
Đọc tiếp
Cho hàm số f(x) liên tục trên R và có bảng xét dấu đạo hàm dưới đây:

Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng − ∞ ; − 3
B. Hàm số đồng biến trên khoảng 0 ; 3
C. Hàm số đồng biến trên khoảng 3 ; + ∞
D. Hàm số nghịch biến trên khoảng 0 ; 3
Cho hàm số yf(x) có đạo hàm yf’(x) liên tục trên R và đồ thị của hàm số f’(x) trên đoạn [-2;6] như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau A.
m
a
x
-
2
;
6
f
x
f
-
2
B.
m...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm y=f’(x) liên tục trên R và đồ thị của hàm số f’(x) trên đoạn [-2;6] như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau
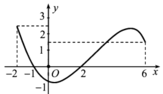
A. m a x - 2 ; 6 f x = f - 2
B. m a x - 2 ; 6 f x = f 6
C. m a x - 2 ; 6 f x = m a x f - 1 ; f 6
D. m a x - 2 ; 6 f x = f - 1
Cho hai hàm số
f
(
x
)
log
2
x
,
g
(
x
)
2
x
. Xét các mệnh đề sau: I. Đồ thị hàm số đối xứng với nhau qua đường thẳng yx II. Tập xác định của hai hàm số trên là R III. Đồ thị hai hàm số cắt nhau tại đúng 1 điểmIV. Hai hàm số đều đồng biến trên tập xác định của nóCó bao nhiêu mệnh đề đúng trong các mệnh đề trên A...
Đọc tiếp
Cho hai hàm số f ( x ) = log 2 x , g ( x ) = 2 x . Xét các mệnh đề sau:
I. Đồ thị hàm số đối xứng với nhau qua đường thẳng y=x
II. Tập xác định của hai hàm số trên là R
III. Đồ thị hai hàm số cắt nhau tại đúng 1 điểm
IV. Hai hàm số đều đồng biến trên tập xác định của nó
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên
A. 2
B. 3
C. 1
D. 4
Cho hàm số f(x) liên tục trên
ℝ
hàm số y f (x) có đồ thị như hình vẽ. Xét hàm số
h
x
2
f
3
x
+
1
-
9
x
2
-
6
x
+
4
. Hãy chọn khẳng định đúng: A. Hàm số h(x) nghịch biến trên
ℝ
B. Hàm số h(x) nghịch biến trên ...
Đọc tiếp
Cho hàm số f(x) liên tục trên ℝ hàm số y = f '(x) có đồ thị như hình vẽ. Xét hàm số h x = 2 f 3 x + 1 - 9 x 2 - 6 x + 4 . Hãy chọn khẳng định đúng:

A. Hàm số h(x) nghịch biến trên ℝ
B. Hàm số h(x) nghịch biến trên - 1 ; 1 3
C. Hàm số h(x) đồng biến trên - 1 ; 1 3
D. Hàm số h(x) đồng biến trên ℝ
Cho hàm số yf(x) có đạo hàm trên đoạn [a;b]. Ta xét các khẳng định sau:1) Nếu hàm số f(x) đạt cực đại tại điểm
x
0
∈
a
;
b
thì
f
x
o
là giá trị lớn nhất của f(x) trên đoạn [a;b]2) Nếu hàm số f(x) đạt cực đại tại điểm
x
0
∈
a...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên đoạn [a;b]. Ta xét các khẳng định sau:
1) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị lớn nhất của f(x) trên đoạn [a;b]
2) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị nhỏ nhất của f(x) trên đoạn [a,b]
3) Nếu hàm số f(x) đạt cực đại tại điểm x 0 và đạt cực tiểu tại điểm x 1 x 0 , x 1 ∈ a ; b thì ta luôn có f x 0 > f x 1
Số khẳng định đúng là?
A. 1
B. 2
C. 0
D. 3
Cho hàm số yf(x)có đạo hàm trên đoạn [a,b]. Ta xét các khẳng định sau:1) Nếu hàm số f(x) đạt cực đại tại điểm
x
0
∈
a
;
b
thì
f
x
o
là giá trị lớn nhất của f(x) trên đoạn[a,b]2) Nếu hàm số f(x) đạt cực đại tại điểm
x
0
∈
a
;...
Đọc tiếp
Cho hàm số y=f(x)có đạo hàm trên đoạn [a,b]. Ta xét các khẳng định sau:
1) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị lớn nhất của f(x) trên đoạn[a,b]
2) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị nhỏ nhất của f(x) trên đoạn [a,b]
3) Nếu hàm số f(x) đạt cực đại tại điểm x 0 và đạt cực tiểu tại điểm x 1 x 0 , x 1 ∈ a ; b thì ta luôn có f x 0 > f x 1
Số khẳng định đúng là?
A. 1
B. 2
C. 0
D. 3



