Xét u = 2 x 3 - 3 x 2 + m
có u ' = 6 x 2 - 6 x ; u ' = 0 ⇔ x = 0 ; x = 1 .
Do đó
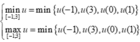
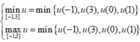

Nếu m - 5 ≥ 0
⇒ m i n - 1 ; 3 f ( x ) = m - 5 ≤ 3 ⇔ m ≤ 8 ⇒ m ∈ 5 , 6 , 7 , 8 .
Nếu m + 27 ≤ 0
⇒ m i n - 1 ; 3 f ( x ) = - m + 27 ≤ 3 ↔ m ≥ - 30 ⇒ m ∈ - 30 ; - 29 ; - 28 ; - 27 .
Vậy m ∈ - 30 , . . . , 8 có tất cả 39 số nguyên thỏa mãn.
Chọn đáp án D.



