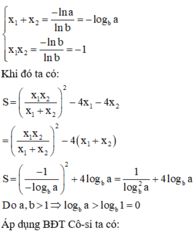
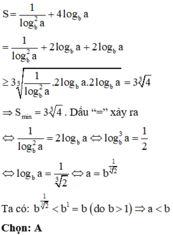
Phương pháp:
+) Lấy loganepe hai vế, đưa phương trình về dạng phương trình bậc hai ẩn x.
+) Tìm điều kiện để phương trình có 2 nghiệm. Áp dụng định lí Vi-ét.
+) Sử dụng BĐT Cô-si cho 3 số không âm đánh giá biểu thức S.
Cách giải:
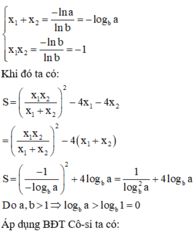
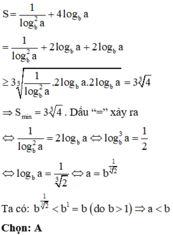
Gọi a là số thực lớn nhất để bất phương trình x 2 - x + 2 + a ln x 2 - x + 1 ≥ 0 nghiệm đúng với mọi x ∈ ℝ . Mệnh đề nào sau đây đúng?
A. a ∈ ( 2 ; 3 ]
B. a ∈ 8 ; + ∞
C. a ∈ ( 6 ; 7 ]
D. a ∈ ( - 6 ; - 5 ]
Gọi a là số thực lớn nhất để bất phương trình x 2 − x − 2 + a ln x 2 − x + 1 ≥ 0 nghiệm đúng với mọi x ∈ ℝ . Mệnh đề nào sau đây đúng?
A. a ∈ 6 ; 7 .
B. a ∈ 2 ; 3 .
C. a ∈ − 6 ; − 5 .
D. a ∈ 8 ; + ∞
Gọi a là số thực lớn nhất để bất phương trình x 2 − x + 2 + a ln x 2 − x + 1 ≥ 0 nghiệm đúng với mọi x ∈ ℝ . Mệnh đề nào sau đây đúng?
A. a ∈ 6 ; 7
B. a ∈ 2 ; 3
C. a ∈ − 6 ; − 5
D. a ∈ 8 ; + ∞
Gọi a là số thực lớn nhất để bất phương trình x 2 - x + 2 + a ln ( x 2 - x + 1 ) ≥ 0 nghiệm đúng với mọi x ∈ R . Mệnh đề nào sau đây đúng?
A. a ∈ ( 8 ; + ∞ )
B. a ∈ ( - 6 ; - 5 )
C. a ∈ ( 6 ; 7 )
D. a ∈ ( 2 ; 3 )
Gọi a là một nghiệm của phương trình ( 26 + 15 3 ) x + 2 ( 7 + 4 3 ) x - 2 ( 2 - 3 ) x = 1 . Khi đó giá trị của biểu thức nào sau đây là đúng?
A. a 2 + a = 2
B. s i n 2 a + cos a = 1
C. 2 + cos a = 2
D. 3 a + 2 a = 5
Cho hàm số y = f ( x ) liên tục trên ℝ và có đồ thị như hình vẽ bên. Xét 4 mệnh đề sau
(1) Hàm số y = f ( x ) đạt cực đại tại x 0 = 0
(2) Hàm số y = f ( x ) có ba cực trị.
(3) Phương trình y = f ( x ) có đúng ba nghiệm phân biệt
(4) Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]
Hỏi trong 4 mệnh đề trên, có bao nhiêu mệnh đề đúng?
A. 1
B. 3
C. 4
D. 2
Cho các số thực x, y với x ≥ 0 thỏa mãn 5 x + 3 y + 5 x y + 1 + x ( y + 1 ) + 1 = 5 - x y - 1 + 1 5 x + 3 y - 3 y . Gọi m là giá trị nhỏ nhất của biểu thức . Mệnh đề nào sau đây là đúng?
A. m ∈ ( 0 ; 1 )
B. m ∈ ( 1 ; 2 )
C. m ∈ ( 2 ; 3 )
D. m ∈ ( - 1 ; 0 )
Cho các mệnh đề :
1) Hàm số y=f(x) có đạo hàm tại điểm x 0 thì nó liến tục tại x 0 .
2) Hàm số y=f(x) liên tục tại x 0 thì nó có đạo hàm tại điểm x 0 .
3) Hàm số y=f(x) liên tục trên đoạn [a;b] và f(a).f(b)<0 thì phương trình f(x) có ít nhất một nghiệm trên khoảng (a;b).
4) Hàm số y=f(x) xác định trên đoạn [a;b] thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
Số mệnh đề đúng là:
A. 2
B. 4
C. 3
D. 1
Cho 2 số thực x;y thỏa mãn x , y ≥ 1 và log 3 x + 1 y + 1 y + 1 = 9 − x − 1 y + 1 Biết giá trị nhỏ nhất của biểu thức P = x 3 + y 3 − 57 x + y là một số thực có dạng a + b 7 , a , b ∈ ℤ . Tính giá trị của a+b
A. -28
B. -29
C. -30
D. -31
