Chọn B.
Ta có ![]()
![]()
Từ (1) và (2) suy ra ![]()
Áp dụng bất đẳng thức Bunyakovsky ta có:
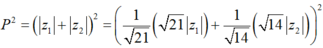
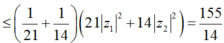
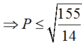 . Vậy
. Vậy 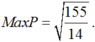
Chọn B.
Ta có ![]()
![]()
Từ (1) và (2) suy ra ![]()
Áp dụng bất đẳng thức Bunyakovsky ta có:
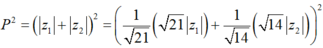
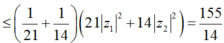
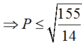 . Vậy
. Vậy 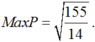
Với hai số phức z 1 và z 2 thỏa mãn z 1 + z 2 = 8 + 6 i và z 1 - z 2 = 2 tìm giá trị lớn nhất P = z 1 + z 2
![]()
![]()
![]()
![]()
Cho hai số phức z 1 , z 2 thỏa mãn z 1 - 3 = 2 và z 2 = i z 1 . Tìm giá trị nhỏ nhất của z 1 - z 2
![]()
![]()
![]()
![]()
Cho 2 số phức z1 và z2 thỏa mãn: |z1 - 5 - i| = 3|z2 + 5 - 2i| = |iz2 - 3|. Giá trị nhỏ nhất của biểu thức P = |z1 - z2| là:
A. -3 - 3 2
B. 3 + 3 2
C. 3 - 3 2
D. -3 + 3 2
Cho hai số phức z 1 ; z 2 thỏa mãn z 1 + 5 = 5 ; z 1 + 1 - 3 i = z 2 - 3 - 6 i . Giá trị nhỏ nhất của z 1 - z 2 là
A. 5 2
B. 7 2
C. 1 2
D. 3 2
Với hai số phức z 1 và z 2 thỏa mãn z 1 + z 2 = 8 + 6 i và z 1 - z 2 = 2 , tìm giá trị lớn nhất P = z 1 + z 2 .
A. P= 4 6
B. P= 2 26
C. P=5+ 3 5
D. P=34+ 3 2
Cho số phức z 1 , z 2 thỏa mãn | z 1 | = 12 và | z 2 - 3 - 4 i | = 5 . Giá trị nhỏ nhất của z 1 - z 2 là
![]()
![]()
![]()
![]()
Cho hai số phức z 1 , z 2 thỏa mãn z 1 + z 2 = 3 5 + 4 5 i , z 1 - z 2 = 3 và biểu thức P = 4 z 1 3 + 4 z 2 3 - 3 z 1 - 3 z 2 + 5 đạt giá trị nhỏ nhất. Tính z 1 + z 2 .
A. 3
B. 3 4
C. 2
D. 1
Cho số phức z 1 thỏa mãn z 1 − 2 2 − z 1 + 1 2 = 1 và số phức z 2 thỏa mãn z 2 − 4 − i = 5 . Tìm giá trị nhỏ nhất của z 1 − z 2
A. 2 5 5 .
B. 5
C. 2 5
D. 3 5 5 .
Cho hai số phức z 1 , z 2 thỏa mãn z 1 − 2 i = 3 và z 2 + 2 + 2 i = z 2 + 2 + 4 i . Giá trị nhỏ nhất của biểu thức P = z 1 − z 2 bằng
A. 1
B. 2
C. 3
D. 4