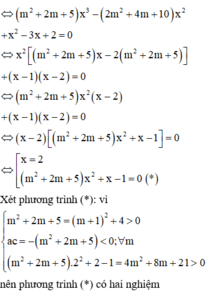
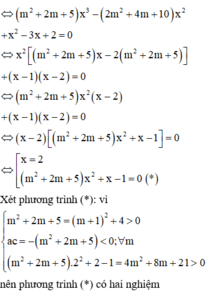
Vì f(x) là hàm đồng biến nên mỗi phương trình (1);(2);(3) đều chỉ có 1 nghiệm duy nhất và ba nghiệm của phương trình này khác nhau.
Từ đó phương trình g f x = 0 có ba nghiệm phân biệt.
Chọn: C
Cho hàm số y=f(x) có đạo hàm f'(x)= x ( x - 1 ) 2 ( x 2 + m x + 9 ) . Có bao nhiêu số nguyên dương m để hàm số y=f(3-x) đồng biến trên khoảng ( 3 ; + ∞ ) .
A. 6.
B. 8.
C. 5.
D. 7.
Cho hàm số f(x)=3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng
A. 1
B. 2.
C. 4.
D. 16.
Cho hai hàm số: f ( x ) = 1 3 x 3 - m + 1 x 2 + m 2 + 2 m + 5 x - 2019 và g ( x ) = ( m 2 + 2 m + 3 ) x 3 - ( 3 m 2 + 6 m + 8 ) x 2 - 4 x + 3 với m là tham số.
Phương trình g(f(x)) = 0 có bao nhiêu nghiệm?
A. 9
B. 6
C. 3
D. 1
Cho hàm số y = 1 3 x 3 - ( m + 1 ) x 2 + ( m + 3 ) x + m - 4 . Tìm m để hàm số y=f(|x|) có 5 điểm cực trị
A. -3<m<-1
B. m>1
C. m>4
D. m>0
Cho hàm số f ( x ) = ∫ 1 x t 3 - ( m + 2 ) t 2 + 2 ( m + 1 ) t - 4 t 4 + 1 d t với x > 1. Trong [-10;10] có bao nhiêu giá trị nguyên của tham số thực m để hàm số đã cho có 3 điểm cực trị
A. 14
B. 15
C. 16
D. 17
Cho hàm số y = f(x) có đạo hàm f ' ( x ) = x ( x - 1 ) 4 ( x 2 + m x + 9 ) với mọi. Có bao nhiêu giá trị nguyên dương của m để hàm số g(x) = f(3 - x) đồng biến trên khoảng 3 ; + ∞
A. 5
B. 6
C. 7
D. Vô số
Cho hàm số y=f(x) thoả mãn f(-2)=3, f(2)=2 và bảng xét dấu của đạo hàm như sau:
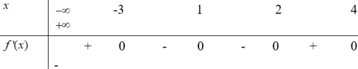
Bất phương trình 3 f ( x ) + m ≤ 4 f ( x ) + 1 + 4 m nghiệm đúng với mọi số thực x ∈ - 2 ; 2 khi và chỉ khi
A. m ∈ - 2 ; - 1
B. m ∈ - 2 ; - 1
C. m ∈ - 2 ; 3
D. m ∈ - 2 ; 3
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x ( x - 2 ) 2 ( 2 x + m + 1 ) ∀ x ∈ ℝ Có bao nhiêu số nguyên âm m để hàm số g ( x ) = f ( x 2 ) đồng biến trên khoảng
A. 5
B. 2
C. 3
D. 4
1. Cho hàm số y=2x-1/x-1 . Lấy M thuộc C với XM=m . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M
2.cho y=x+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau
3. cho y = x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5)
4 . cho y = x+1/x-1 . CMR (d) : 2x-y+m=0 luôn cắt C tại A,B trên 2 nhánh của (C) . tìm m để AB ngắn nhất
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x ( x - 2 ) 2 ( 2 x + m + 1 ) với mọi x ∈ R . Có bao nhiêu số nguyên âm m để hàm số g ( x ) = f ( x 2 ) đồng biến trên khoảng ?
A. 5.
B. 2.
C. 3.
D. 4.
