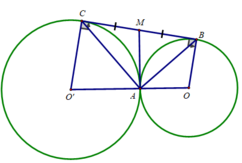
a) Ta có:
OB // O'C ( cùng vuông góc với d)
⇒ Tứ giác OBCO' là hình thang vuông
⇒ ∠(BOO') + ∠(CO'O) = 180 0
Δ CO'A cân tại O' có:
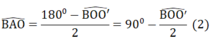
Từ (1) và (2):
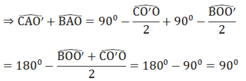
Lại có: ∠(CAO') + ∠(BAO) + ∠(BAC) = 180 0 ⇒ ∠(BAC) = 180 0 - 90 0 = 90 0
⇒ ΔABC vuông tại A.

a) Ta có:
OB // O'C ( cùng vuông góc với d)
⇒ Tứ giác OBCO' là hình thang vuông
⇒ ∠(BOO') + ∠(CO'O) = 180 0
Δ CO'A cân tại O' có:
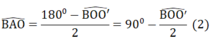
Từ (1) và (2):
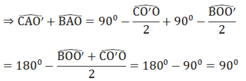
Lại có: ∠(CAO') + ∠(BAO) + ∠(BAC) = 180 0 ⇒ ∠(BAC) = 180 0 - 90 0 = 90 0
⇒ ΔABC vuông tại A.
cho hai đường tròn (O;R) và (O;r) tiếp xúc ngoài tại A. Một đường thẳng (d) tiếp xúc với cả hai đường tròn trên tại B và C với B ∈ (O), C ∈ (O’).
a) Chứng minh tam giác ABC vuông
b) Gọi M là trung điểm của BC. Chứng minh MA là tiếp tuyến chung của hai đường tròn (O) và (O‘).
Cho hai đường tròn (O;R) và (O;r) tiếp xúc ngoài tại A. Một đường thẳng (d) tiếp xúc với cả hai đường tròn trên tại B và C với B ∈ (O), C ∈ (O’).
b) Gọi M là trung điểm của BC. Chứng minh MA là tiếp tuyến chung của hai đường tròn (O) và (O‘).
Cho 2 đường tròn (O;R) và (O',r) tiếp xúc ngoài tại A. Một đường thẳng (d) tiếp xúc với cả 2 đường tròn trên tại B và C với B thuộc (O) và C thuộc (O'):
a) Chứng minh tam giác ABC vuông.
b) Gọi M là trung điểm của BC. Chứng minh MA là tiếp tuyến chung của 2 đường tròn.
Cho hai đường tròn (O;R) và (O;R) tiếp xúc ngoài tại A. Một đường thẳng (d) tiếp xúc với (O) và (O') theo thứ tự ở B và C.
a, Chứng minh \(\Delta ABC\)vuông
b, Chứng minh AM là tiếp tuyến chung của 2 đường tròn(O) và (O')
c, Kẻ AH vuông góc BC tại H. Chứng minh\(AH\le\frac{2R.R'}{R+R'}\)
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (O) đường kính BH và đường tròn tâm O' đường kính CH, hai đường tròn này cắt AB, AC thứ tự tại E và F
a, Tứ giác AEHF là hình gì?
b, Chứng minh EF là tiếp tuyến chung của (O) và (O’)
c, Chứng minh đường tròn đường kính OO' tiếp xúc với EF
d, Cho đường tròn tâm I bán kính r tiếp xúc với EF, (O) và (O’). Tính r theo BH và CH?
Bài 2: Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. 1 đường thẳng d tiếp xúc với (O) và (O') lần lượt tại B và C.
a) CM: tam giác ABC vuông
b) Gọi M là trung điểm BC. C/m: AM là tiếp tuyến trung của hai đường tròn
c) C/m: góc OMO' = 90°
d) Các tia BA, CA lần lượt cắt đường tròn (O) và (O') tại D và E. Chứng minh: Diện tích tam giác ADE = Diện tích tam giác ABC
Cho 2 đường tròn (O) và (O') tiếp xúc ngoài tại A. Một đường thẳng (d) tiếp xúc với đường tròn (O) và (O') thứ tự tại B và A. I là giao điểm của (d) và tiếp tuyến tại A của đường tròn (O) và (O').
a, chứng minh: tam giác ABC vuông
b, chứng minh: góc OIO'=90 độ
c, các tia BA và CA cắt đường tròn (O') và (O) tại D và E. chứng minh: góc ADE= góc ADC
Cho đường tròn (O,R) tiếp xúc ngoài với (O’,r) tại A. Một tiếp tuyến chung ngoài của hai đường tròn (O) và (O’) lần lượt tiếp xúc với hai đường tròn tại B và C. Vẽ AH vuông góc với BC tại H
a) Tính BC theo R và r
b) Chứng minh rằng ba đường thẳng OB, O’C và AH đồng qui tại trung điểm của AH
Cho đường tròn (O,R) tiếp xúc ngoài với (O’,r) tại A. Một tiếp tuyến chung ngoài của hai đường tròn (O) và (O’) lần lượt tiếp xúc với hai đường tròn tại B và C. Vẽ AH vuông góc với BC tại H
a) Tính BC theo R và r
b) Chứng minh rằng ba đường thẳng OB, O’C và AH đồng qui tại trung điểm của AH