Cho hai đường tròn đồng tâm (O;R) và (O;r) với R>r. Lấy A và E là hai điểm thuộc đường tròn (O;r), trong đó A di động (với A#E)A khácE. Qua E vẽ một đường thẳng vuông góc với AE cắt đường tròn (O;R) ở B và C. Gọi M là trung điểm của đoạn AB.
a)Chứng minh \(EB^2+EC^2+EA^2\) không phụ thuộc vị trí điểm A.
b)Chứng minh rằng khi điểm A di động trên đường tròn (O;r) và A#E thì đường thẳng CM luôn đi qua một điểm cố định (gọi tên điểm cố định là J).
c)Trên tia AJ đặt một điểm H sao cho \(AH=\frac{3}{2}AJ\). Khi A di động trên đường tròn (O;) thì điểm H di động trên đường nào?
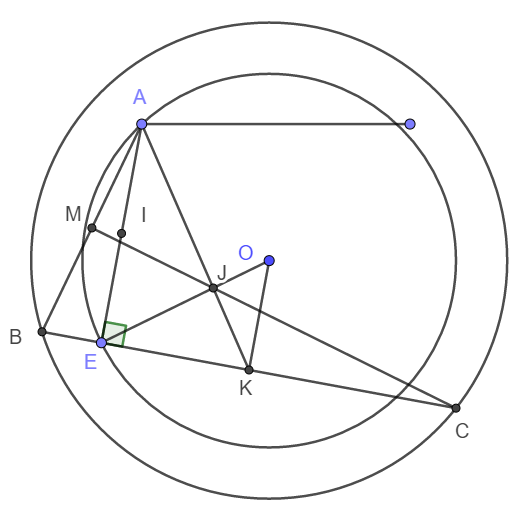
a) Gọi I, K lần lượt là trung điểm của AE và BC.
Ta có : \(EB^2=\left(BK-EK\right)^2;EC^2=\left(KC+EK\right)^2\)
\(\Rightarrow EB^2+EC^2=2\left(BK^2+EK^2\right)=2\left(BO^2-OK^2+OE^2-OK^2\right)\)
\(=2\left(R^2+r^2\right)-4OK^2\)
\(AE^2=4AI^2=4\left(r^2-OI^2\right)\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+6r^2-4\left(OI^2+OK^2\right)\)
Mà OIEK là hình chữ nhật nên \(OI^2+OK^2=OE^2=r^2\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+2r^2\) không đổi.
b) Giả sử EO giao với AK tại J.
Vì IOEK là hình chữ nhật nên OK song song và bằng EI. Vậy nên OK song song và bằng một nửa AE.
Do đó \(\frac{JE}{JO}=\frac{AJ}{JK}=\frac{AE}{OK}=2\)
Vì OE cố định nên J cố định; Vì AK là trung tuyến của tam giác ABC nên J là trọng tâm tam giác ABC
Suy ra J thuộc MC.
Vậy MC đi qua J cố định.
c) Vì AK = 3/2AJ nên H trùng K.
Do đó OH vuông góc BC. Suy ra H thuộc đường tròn đường kính OE.











