Chọn A.
Hai điểm A(1;2) và B(4;6) ⇒ AB = 5
Gọi M(0;m).
Vì diện tích tam giác MAB bằng 1
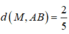
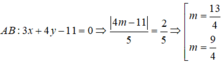
Chọn A.
Hai điểm A(1;2) và B(4;6) ⇒ AB = 5
Gọi M(0;m).
Vì diện tích tam giác MAB bằng 1
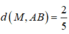
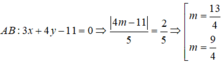
Cho hai điểm A(1; 2) và B( 4; 6).Hỏi có mấy điểm M trên trục tung sao cho diện tích tam giác MAB bằng 1 ?
A. 0
B. 1
C. 2
D. 3
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(-1;2), B(3;4), C(1;-6). Tìm quỹ tích
các điểm M sao cho hai tam giác MAB và MAC có diện tích bằng nhau.
Trên mặt phẳng Oxy, cho hai điểm A(1; 3), B(4; 2).
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB;
b) Tính chu vi tam giác OAB.
c) Chứng tỏ OA vuông góc với AB và từ đó tính diện tích tam giác OAB.
Trong mặt phẳng với hệ tọa độ Oxy , cho điểm M (2;1) và đường thẳng d: x-y+1=0. Viết phương trình đường tròn đi qua M cắt d ở 2 điểm A, B phân biệt sao cho tam giác MAB vuông tại M và có diện tích bằng 2.
Trong mặt phẳng tọa độ Oxy cho hai điểm A ( 12 ) ; B ( -1 ; 1 ) . Điểm M thuộc trục Oy thỏa mãn tam giác MAB cân tại M . Khi đó độ dài đoạn OM bằng?
Cho điểm A (-5; 4), đường thẳng d qua A,d cắt 2 tia Ox, Oy lần lượt tại M(m; 0), N (n; b) sao cho tam giác MNO (O là gốc tọa độ) có diện tích nhỏ nhất.
Giúp e với ạ
Cho tam giác ABC với A = (1; 4), B = (2; – 5 ), C = (0; 7). Điểm M nằm trên trục Ox sao cho vectơ M A → + M B → + M C → có độ dài nhỏ nhất. Tọa độ điểm M là:
A. M(5; 0)
B. M(–2; 0)
C. M(3; 0)
D. M(1; 0)
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có đỉnh A(2;-3) , B(3:-2) và trọng tâm G nằm trên đường thẳng d: 3x-y-8=0
a, Tìm tọa độ M trên trục hoành sao cho d(M;AB) = \(\sqrt{2}\)
b, tìm tọa độ điểm C biết tam giác ABC có diện tích bằng \(\frac{3}{2}\)
Cho A( 2;2) ; B( 5;1) và đường thẳng d: x- 2y + 8= 0. Điểm C nằm trên d và C có hoành độ dương sao cho diện tích tam giác ABC bằng 17. Tọa độ của C là:
A.(8; 10)
B.(12; 10)
C.(6;6)
D.(6; 8)