Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Cạnh bên SA vuông góc với đáy và SC tạo với (SAD) góc 30 o . Gọi G là trọng tâm tam giác SAB. Tính khoảng cách từ G đến mặt phẳng (SCD).
Cho hình chóp S.ABCD, SA vuông góc (ABCD), SC = √3 . ABCD là hình vuông cạnh a, tâm O. G là trọng tâm tam giác SCD. Tính khoảng cách giữa OG và AD
Cho hình chóp S.ABCD có ABCD là hình vuông tâm O, cạnh a SA vuông góc với mặt phẳng (ABCD) và SA=a căn 2. Tính khoảng cách từ:
a) C đến mặt phẳng (SAB).
b) từ A đến (SCD).
c) Từ O đến (SCD).
d) Khoảng cách giữa hai đường thẳng AB và SC.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh A. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm I thuộc đoạn AB sao cho BI 2AI. Góc giữa mặt bên (SCD) và mặt đáy (ABCD) bằng
60
0
. Tính khoảng cách giữa hai đường thẳng AD và SC.
A
.
93
31
a
B
.
3
93...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh A. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm I thuộc đoạn AB sao cho BI = 2AI. Góc giữa mặt bên (SCD) và mặt đáy (ABCD) bằng 60 0 . Tính khoảng cách giữa hai đường thẳng AD và SC.
A . 93 31 a
B . 3 93 31 a
C . 93 31
D . 3 93 31 a
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AD a, AB 2a, BC 3a, SA 2a. H là trung điểm cạnh AB, SH là đường cao của hình chóp S.ABCD, Tính khoảng cách từ điểm A đến mp (SCD)
A
.
a
30
7
B
.
a
30
10
C
.
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AD = a, AB = 2a, BC = 3a, SA = 2a. H là trung điểm cạnh AB, SH là đường cao của hình chóp S.ABCD, Tính khoảng cách từ điểm A đến mp (SCD)
A . a 30 7
B . a 30 10
C . a 13 10
D . a 13 7
Cho hình chóp S.ABCD có đáy là nửa lục giác đều ABCD nội tiếp trong đường tròn đường kính AD = 2a và có cạnh SA vuông góc với mặt phẳng đáy (ABCD) với SA = a√6.
a) Tính khoảng cách từ A và B đến mặt phẳng (SCD).
b) Tính khoảng cách từ đường thẳng AD đến mặt phẳng (SBC).
Hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác đáy ABC.
a) Tính khoảng cách từ S tới mặt phẳng đáy (ABC).
b) Tính khoảng cách giữa hai đường thẳng AB và SG.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 6a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trọng tâm G của tam giác ABD d(G,(SAD))a (tham khảo hình vẽ bên). Tính khoảng cách giữa hai đường thẳng SD và BC. A. 2a B. 3a C. 4a D.
3
a
2
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 6a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trọng tâm G của tam giác ABD d(G,(SAD))=a (tham khảo hình vẽ bên). Tính khoảng cách giữa hai đường thẳng SD và BC.
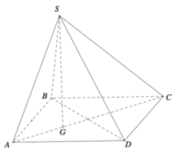
A. 2a
B. 3a
C. 4a
D. 3 a 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AD=2a. Cạnh bên SA=2a và vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng AB và SD
A. a
B. 2a
C. 2 a 5
D. a 2




