x+3y\(\ge\)1=>x\(\ge\)1-3y
Suy ra: A\(\ge\)(1-3y)2+y2=1-6y+9y2+y2=10y2-6y+1=\(10.\left(y^2-\frac{3}{5}y+\frac{1}{10}\right)\)
\(=10.\left(y^2-2.y.\frac{3}{10}+\frac{9}{100}+\frac{1}{100}\right)=10.\left(x-\frac{3}{10}\right)^2+\frac{1}{10}\ge\frac{1}{10}=0,1\)
Vậy GTNN của A là 0,1 tại x=0,3




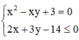 Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu
Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu