Chọn A.
Ta có: ![]()
![]()
Vậy f'(1) + f'(-1) + 4f(0) = 6 + 6 + 4.(-2) = 4
Chọn A.
Ta có: ![]()
![]()
Vậy f'(1) + f'(-1) + 4f(0) = 6 + 6 + 4.(-2) = 4
Cho f(x) = x5 + x3 - 2x - 3 . Tính f’(1) + f’(-1) + 4f(0).
A. 4.
B. 7.
C. 6.
D. 5.
xét sự biến thiên của hàm số a)f'(x)=(x+1)⁷(x²-4x)(x-2)³x⁵ b)f'(x)=(x²-7x+6)(-2x+7)/(x-1)³(x-4)² c)f'(x)=(x²-6x+5)(x-1)⁷/x²+3x+2
xét sự biến thiên của hàm số a)f'(x)=(x+1)⁷(x²-4x)(x-2)³x⁵ b)f'(x)=(x²-7x+6)(-2x+7)/(x-1)³(x-4)² c)f'(x)=(x²-6x+5)(x-1)⁷/x²+3x+2
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
Cho hàm số f(x) thỏa mãn ∫ 1 2 ( 2 x + 3 ) . f ' ( x ) d x = 15 và 7 . f ( 2 ) - 5 . f ( 1 ) = 8 Tính I= ∫ 1 2 f ( x ) d x .
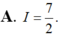
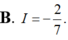

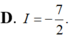
Cho hàm số f(x) xác định trên ℝ \ - 2 ; 1 thỏa mãn f ' ( x ) = 1 x 2 + x - 2 ; f ( 0 ) = 1 3 và f(3)-f(-3) = 0 Tính giá trị của biểu thức T = f(-4)+f(-1)-f(4)
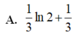
![]()
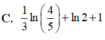
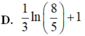
Giá trị nhỏ nhất của hàm số f(x) = x +1/x trên nửa khoảng [2;+••] A:2 B:5/2 C:0 D:7/2
Cho f(x) = \(\dfrac{1}{x-1}\) thỏa F(0)=2, F(2)=3. Tính F(3)+F(-3)