Chọn B
f ( x ) = ∫ f ' ( x ) d x = 3 x + 5 cos x + C
Do f ( 0 ) = 10 ⇔ C = 5
Vậy f ( x ) = 3 x + 5 cos x + 5 ⇒ f ( π ) = 3 π
Chọn B
f ( x ) = ∫ f ' ( x ) d x = 3 x + 5 cos x + C
Do f ( 0 ) = 10 ⇔ C = 5
Vậy f ( x ) = 3 x + 5 cos x + 5 ⇒ f ( π ) = 3 π
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = 2 cos x - 1 sin 2 x trên khoảng 0 ; π . Biết rằng giá trị lớn nhất của F(x) trên khoảng 0 ; π là 3 . Chọn mệnh đề đúng trong các mệnh đề sau?

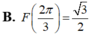
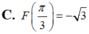
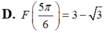
Giá trị lớn nhất của hàm số f(x) = sin x + cos 2x trên [0; π ] là
A. 5 4
B. 1
C. 2
D. 9 8
Cho f(x)= log 5 ( sin x ) , x ∈ ( 0 ; π / 2 ) . Tính f'(x)
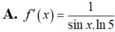
![]()
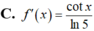
![]()
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
Tìm hàm số F(x) sao cho F’(x) = f(x) nếu:
f(x) = 1/(cosx)2 với x ∈ ((-π)/2; π/2). f x = 1 cos x 2 v ớ i x ∈ - π 2 ; π 2
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình bên. Phương trình f( 2 sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn - π ; π khi và chỉ khi
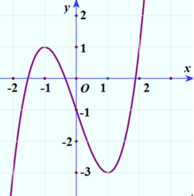
A. m ∈ - 3 ; 1
B. m ∈ - 3 ; 1
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]
Cho hàm f(x) có đạo hàm trên đoạn [ 0 ; π ] , f ( 0 ) = π , ∫ 0 π f ' ( x ) dx = 3 π . Tính f ( π )
![]()
![]()
![]()
![]()
Cho hàm số f(x) thỏa mãn f'(x) = 3 - 5sinx và f(0) = 10. Mệnh đề nào dưới đây đúng ?
![]()
![]()
![]()
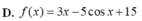
Gọi VV là thể tích vật thể tròn CC xoay được tạo thành khi quay miền D được giới hạn bởi các đường y=f\left(x\right);y=0;x=a;x=by=f(x);y=0;x=a;x=b quanh trục OxOx. Khẳng định nào dưới đây đúng?
V=\int_a^bf^2\left(x\right)\text{d}xV=∫abf2(x)dx.
V=\pi\int_a^bf^2\left(x\right)\text{d}xV=π∫abf2(x)dx.
V=\pi^2\int_a^bf\left(x\right)\text{d}x.V=π2∫abf(x)dx.
V=\pi\int_a^bf\left(x\right)\text{d}xV=π∫abf(x)dx.