Các câu hỏi tương tự
Cho hàm số
f
(
x
)
l
n
(
x
2
-
2
x
+
3
)
. Tập nghiệm của bất phương trình f(x)0 là A.
(
2
;
+
∞
)
. B.
(
-
1
;
+
∞
)
. C.
(
-
2
;
+
∞
)...
Đọc tiếp
Cho hàm số f ( x ) = l n ( x 2 - 2 x + 3 ) . Tập nghiệm của bất phương trình f'(x)>0 là
A. ( 2 ; + ∞ ) .
B. ( - 1 ; + ∞ ) .
C. ( - 2 ; + ∞ ) .
D. ( 1 ; + ∞ ) .
Cho hàm số f(x)-1/3x3 + 4x2-7x+2. Tập nghiệm của bất phương trình:
f
(
x
)
≥
0
là
Đọc tiếp
Cho hàm số f(x)=-1/3x3 + 4x2-7x+2. Tập nghiệm của bất phương trình: f ' ( x ) ≥ 0 là
![]()
![]()
![]()
![]()
Cho F(x) là một nguyên hàm của hàm số
1
e
x
+
1
, thỏa mãn
F
(
0
)
-
ln
2
. Tìm tập nghiệm S của phương trình
F
(
x
)
+
l
n
(
e
x
+
1
)
3
A. ...
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số 1 e x + 1 , thỏa mãn F ( 0 ) = - ln 2 . Tìm tập nghiệm S của phương trình F ( x ) + l n ( e x + 1 ) = 3
A. S = 3
B. S = - 3
C. S = ∅
D. S = ± 3
Cho các mệnh đề sau đây:(1) Hàm số
f
(
x
)
log
2
2
x
-
log
2
x
4
+
4
có tập xác định
D
[
0
;
+
∞
)
(2) Hàm số
y
log
a
x
có tiệm cận ngang(3) Hàm số
y
log
a
x
;
...
Đọc tiếp
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
Cho hàm số
f
(
x
)
l
n
(
x
2
-
3
x
)
. Tập nghiệm S của phương trình f(x) 0 là: A. S
∅
B. S
3
2
C. S {0;3} D. S
-
∞
;
0
∪
3...
Đọc tiếp
Cho hàm số f ( x ) = l n ( x 2 - 3 x ) . Tập nghiệm S của phương trình f'(x) = 0 là:
A. S = ∅
B. S = 3 2
C. S = {0;3}
D. S = - ∞ ; 0 ∪ 3 ; + ∞
Cho hàm số y f (x) liên tục trên R có đồ thị như hình vẽ. Biết trên
(
-
∞
;
-
3
)
∪
(
2
;
+
∞
)
t
h
ì
f
(
x
)
0
. Số nghiệm nguyên thuộc (-10; 10) của bất phương trình
[
f
(
x
)...
Đọc tiếp
Cho hàm số y = f (x) liên tục trên R có đồ thị như hình vẽ.
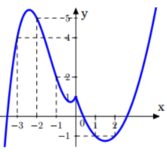
Biết trên ( - ∞ ; - 3 ) ∪ ( 2 ; + ∞ ) t h ì f ' ( x ) > 0 . Số nghiệm nguyên thuộc (-10; 10) của bất phương trình [ f ( x ) + x - 1 ] ( x 2 - x - 6 ) > 0 là
A. 9
B. 10
C. 8
D. 7
Cho hàm số
g
(
x
)
x
2
+
1
và hàm số
f
(
x
)
x
3
-
3
x
2
+
1
. Tìm m để phương trình
f
(
g
(
x
)
)
-
m
0
có 4 nghiệm phân biệt. A.
-...
Đọc tiếp
Cho hàm số g ( x ) = x 2 + 1 và hàm số f ( x ) = x 3 - 3 x 2 + 1 . Tìm m để phương trình f ( g ( x ) ) - m = 0 có 4 nghiệm phân biệt.
A. - 3 < m < 1
B. - 3 < m ≤ 1
C. - 3 ≤ m ≤ - 1
D. m > - 1
Cho hàm số
f
(
x
)
x
3
-
3
x
2
+
5
x
+
1
Hàm số yg(x) có bảng biến thiên như sauBiết rằng
a
,
b
∈
R
và ab;g(a).g(b)0 Phương trình g(f(x))0 có tất cả bao nhiêu nghiệm thực? A. 3 B. 9 C. 5 D. 1
Đọc tiếp
Cho hàm số f ( x ) = x 3 - 3 x 2 + 5 x + 1 Hàm số y=g(x) có bảng biến thiên như sau
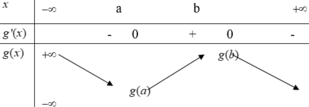
Biết rằng a , b ∈ R và a<b;g(a).g(b)<0 Phương trình g(f(x))=0 có tất cả bao nhiêu nghiệm thực?
A. 3
B. 9
C. 5
D. 1
Cho hàm số yf(x). Đồ thị hàm số yf’(x) như hình vẽ. Đặt
g
(
x
)
3
f
(
x
)
-
x
3
+
3
x
-
m
, với m là tham số thực. Điều kiện cần và đủ để bất phương trình g(x)≥0 nghiệm đúng với
∀
x
∈
-
3
;
3...
Đọc tiếp
Cho hàm số y=f(x). Đồ thị hàm số y=f’(x) như hình vẽ. Đặt g ( x ) = 3 f ( x ) - x 3 + 3 x - m , với m là tham số thực. Điều kiện cần và đủ để bất phương trình g(x)≥0 nghiệm đúng với ∀ x ∈ - 3 ; 3 là
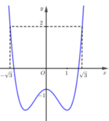
A. m < 3 f 3
B. m > 3 f 3
C. m ≤ 3 f 3
D. m ≥ 3 f 3
Cho hàm số
y
f
x
2
x
2
−
7
x
+
6
x...
Đọc tiếp
Cho hàm số y = f x = 2 x 2 − 7 x + 6 x − 2 k h i x < 2 a + 1 − x 2 + x k h i x ≥ 2 . Biết a là giá trị để hàm số f(x) liên tục tại x 0 = 2 , tìm nghiệm nguyên của bất phương trình − x 2 + a x + 7 4 > 0 .
A. 1
B. 4
C. 3
D. 2