Cho đường tròn (T) đường kính AB=2R. Trên tia đối của tia AB lấy điểm O sao cho A là trung tâm của OB. Trên đường thẳng vuông góc với đường thẳng AB tại O lấy điểm M bất kì Các tia MA,MB lần lượt căt (T) tại điểm thứ hai là C và E
1. CM bốn điểm O, E, A, M cùng nằm trên một đường tròn
2. Tia OE cắt T tại điểm thứ hai là F. CM OE. OF+BE. BM=16R2
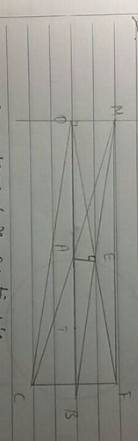
ta có △ AEB nội tiếp (T) có AB là đường kính -> AE vuông EB hay AE vuông ME
xét tứ giác OAEM có góc MOA=góc AEM = 90độ → tứ giác OAEM nội tiếp → 4 điểm O,A,E,M cùng nằm trên một đường tròn










