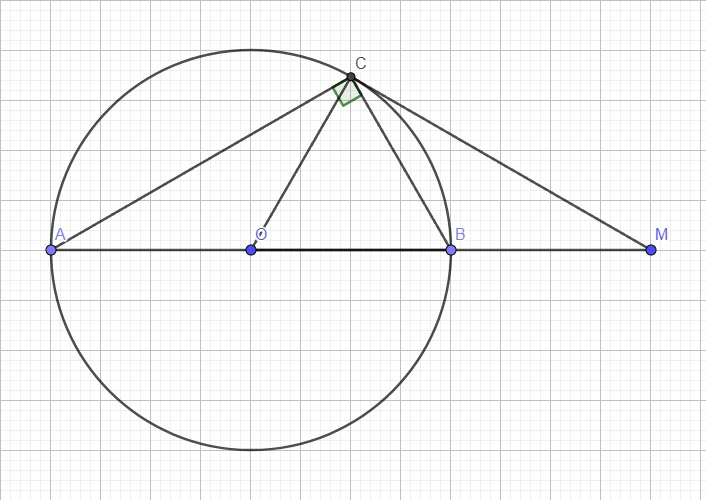
a.
Do \(OB=OC=R\Rightarrow\Delta OBC\) cân tại O
Lại có AB là đường kính \(\Rightarrow\widehat{ACB}=90^0\) (góc nt chắn nửa đường tròn)
\(\Rightarrow\widehat{CBA}=90^0-\widehat{ACB}=60^0\)
\(\Rightarrow\Delta OBC\) đều
\(\Rightarrow BC=BO\Rightarrow BC=BO=BM\)
\(\Rightarrow O,C,M\) cùng thuộc đường tròn đường kính OM
\(\Rightarrow\widehat{OCM}=990^0\) (góc nt chắn nửa đường tròn)
\(\Rightarrow MC\perp OC\Rightarrow MC\) là tiếp tuyến của (O)
b.
Theo cmt \(\Delta OBC\) đều \(\Rightarrow\widehat{COB}=60^0\)
Trong tam giác vuông OCM:
\(tan\widehat{COB}=\dfrac{MC}{OC}\Rightarrow MC=OC.tan\widehat{COB}\)
\(\Rightarrow MC=R.tan60^0=R\sqrt{3}\)
a/
ta có
\(\widehat{ACB}=90^o\) (góc nt chắn nửa đường tròn)
Xét tg vuông ABC có
\(\widehat{ABC}=90^o-\widehat{CAB}=90^o-30^o=60^o\)
Xét tg OBC có
OB=OC => tg OBC cân tại O \(\Rightarrow\widehat{OCB}=\widehat{ABC}=60^o\Rightarrow\widehat{BOC}=60^o\)
=> tg OBC là tg đều
Xét tg ABC và tg MOC có
BC=OC=R
AB=OM=2R
\(\widehat{ABC}=\widehat{MOC}=60^o\)
=> tg ABC = tg MOC (c.g.c)
\(\Rightarrow\widehat{BAC}=\widehat{OCM}=90^o\Rightarrow MC\perp OC\)
b/
Xét tg vuông MOC có
\(MC=\sqrt{OM^2-OC^2}\) (Pitago)
\(\Rightarrow MC=\sqrt{4R^2-R^2}=R\sqrt{3}\)