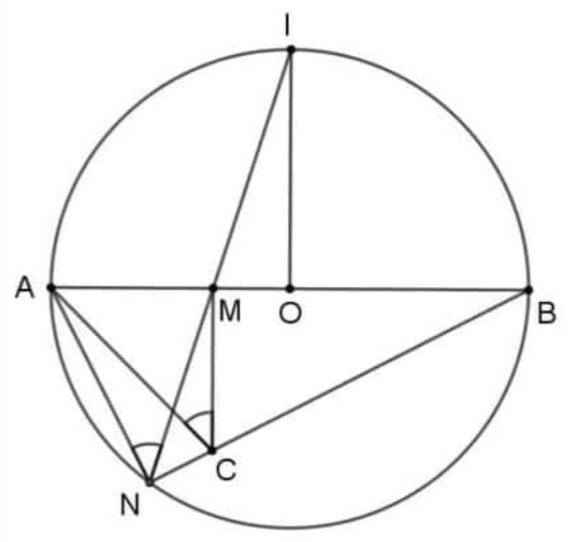
Cho đường tròn (O;R)), đường kính AB. Gọi I là điểm chính giữa cung AB. Lẫy điểm M bất kì trên đoạn thẳng OA (M khác OO và A)A). Tia IM cắt đường tròn tại điểm thứ hai N. Đường thẳng qua M, vuông góc với AB cắt đoạn thẳng BN tại C. a) Chứng minh bốn điểm A, M,C,N cùng thuộc một đường tròn. b) Tính số đo góc AMN và chứng minh AM=MC. c) Khi M thay đổi trên đoạn OA, chứng minh MN<R.
a) dễ thấy \(\widehat{AMC}\) \(=\) \(90^o\) xét (O) có đường kính \(AB\) \(\Rightarrow\) \(\widehat{ANB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\) \(\widehat{ANB}\) \(=90^o\) hay \(\widehat{ANC}\) \(=90^o\) . tứ giác \(ANCM\) có :
\(\widehat{AMC}\) \(+\) \(\widehat{ANC}\) \(=90^o+90^o=180^o\) \(\Rightarrow\) tứ giác \(ANCM\) nội tiếp 4 điểm \(A,N,C,M\) cùng \(\in\) 1 đường tròn
b) vì \(AB\) là đường kính của (O) \(\Rightarrow\) \(\stackrel\frown{AB}\) \(=180^o\)
mà \(I\) là điểm chính giữa của \(\stackrel\frown{AB}\)
\(\Rightarrow\) \(A=\dfrac{\stackrel\frown{AB}}{2}\) \(=\dfrac{180^o}{2}=90^o\)
có \(\widehat{ANI}\) là góc nội tiếp chắn \(\stackrel\frown{IA}\)
\(\Rightarrow\) \(\widehat{ANI}\) \(=\dfrac{1}{2}\) ; \(A=\dfrac{1}{2}.90^o\) \(=45^o\) hay \(\widehat{ANM}\) \(=45^o\) . mặt khác , tứ giác \(ANCM\) nội tiếp \(\Rightarrow\) \(\widehat{ANM}\) \(=\) \(\widehat{ACM}\) mà \(\widehat{ANM}\) \(=45^o\) \(\Leftrightarrow\) \(\widehat{ACM}\) \(=45^o\) lại có \(\Delta ACM\) cuông tại \(M\) \(\Rightarrow\) \(\Delta ACM\) vuông cân tại \(M\)
\(\Rightarrow\) \(AM=CM\)
c) kẻ đường kính \(ID\) của (O) :
có : \(MN=IN-IM\) mà \(IN\) là dây của (O) nên hiển nhiên \(IN\le ID\) nhưng do \(IN\) không qua (O) nên \(IN< ID\) (1) , dễ dàng chứng minh \(IO\perp AB\) tại \(O\)
do vậy : \(\Delta IOM\) vuông tại (O) \(\Rightarrow\) \(IM>IO\) ( không xảy ra dấu " = " vì \(M\) không trùng với \(O\) )
\(\Leftrightarrow\) \(-IM< -IO\) (2)
từ (1) và (2)
\(\Rightarrow\) \(IN-IM< ID-IO\) \(\Leftrightarrow\) \(MN< OD\) \(=R\)
vậy ta có \(đpcm\)