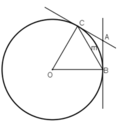
+ ΔOBC có OB = OC = BC (= R)
⇒ ΔOBC là tam giác đều

+ 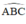 là góc tạo bởi tiếp tuyến BA và dây BC
là góc tạo bởi tiếp tuyến BA và dây BC
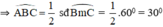
+ 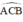 là góc tạo bởi tiếp tuyến AC và dây CB
là góc tạo bởi tiếp tuyến AC và dây CB
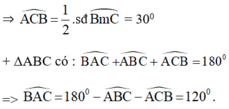

+ ΔOBC có OB = OC = BC (= R)
⇒ ΔOBC là tam giác đều

+ 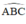 là góc tạo bởi tiếp tuyến BA và dây BC
là góc tạo bởi tiếp tuyến BA và dây BC
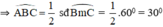
+ 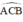 là góc tạo bởi tiếp tuyến AC và dây CB
là góc tạo bởi tiếp tuyến AC và dây CB
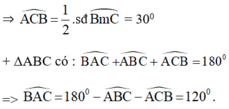
Cho đường tròn (O; R) và dây cung BC = R. Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau ở A. Tính: ABC ^ , BAC ^
Cho đường tròn (O; R) và dây cung BC = R. Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau ở A. Tính: A B C ^ , B A C ^
Cho đường tròn (o;R) và dây cung BC=R. Hai tiếp tuyến của đường tròn (o) tại B,Có cắt nhau ở A a, Chứng minh ABOC là tứ giác nội tiếp b, Tính ABC^?
Cho đường tròn (O) và dây BC = 2 R. Hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại A. Tính góc A B C ^
A. 45 °
B. 30 °
C. 60 °
D. 75 0
Cho đường tròn (O; R) với dây cung BC cố định. Điểm A thuộc cung lớn BC. Đường phân giác của B A C ^ cắt đường tròn (O)tại D. Các tiếp tuyến của đường tròn (O; R) tại C và D cắt nhau tại E. Tịa CD cắt AB tại K, đường thẳng AD cắt CE tại I
a, Chứng minh BC song song DE
b, Chứng minh AKIC là tứ giác nội tiếp
c, Cho BC = R 3
cho đường tròn o và dây cung ab với góc aob=120 hai tiếp tuyến tại a và b của đường tròn o cắt nhau tại c
a)CM tam giác abc là tam giác đều và tính diện tích abc theo R
b)lấy m thuộc cung nhỏ ab của đường tròn. vẽ tiếp tuyến m cắt ac và bc tại d và e. CM ad+be=de
c)CM GÓC dce=doe
Cho đường tròn tâm O bán kính R, dây BC khác đường kính. Hai tiếp tuyến của đường tròn ( O,R) tại B và tại C cắt nhau tại A. Kẻ đường tròn CD, kẻ BH vuông góc với CD tại H. A. Chứng minh bốn điểm A,B,O,C cùng thuộc 1 đường tròn. B. chứng minh AO vuông góc với BC. Cho biết R=15cm, BC=24cm. Tính AB,OA. C. Gọi I là giao điểm của AD và BH,E là giao điểm của BC và AC. Chứng minh IH=IB
Cho đường tròn (O;R) có đường kính AC và dây cung BC = R.
a) C/m ∆ABC vuông tại B và tính số đo của góc A và độ dài AB theo R.
b) Đường thẳng qua O và vuông góc với AB tại H cắt tiếp tuyến tại A của đường tròn (O) ở D. C/m DB là tiếp tuyến của đường tròn (O).
c) Vẽ dây BE⊥AC tại M. C/m tứ giác OBCE là hình thoi và tính diện tích tứ giác OBCE theo R.
d) Tiếp tuyến tại C của (O) cắt DB tại K. C/m AK, CD, BE đồng quy.
Cho đường tròn (O;R) và dây cung BC sao cho góc BOC = 90 độ. Tiếp tuyến với đường tròn tại B và C cắt nhau ở A. Trên cung nhỏ BC lấy điểm I, qua I vẽ tiếp tuyến với đường tròn cắt AB, AC lần lượt tại M và N.
a) Chứng minh tứ giác ABOC là hình vuông
b) OM, ON cắt BC lần lượt tại H và K. Chứng minh tứ giác OHNC nội tiếp