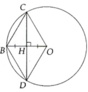
Chứng minh được ∆BOC và ∆BOD là tam giác đều nên suy ra được sđ cung nhỏ C D ⏜ = 120 0 và sđ cung lớn C D ⏜ = 240 0

Chứng minh được ∆BOC và ∆BOD là tam giác đều nên suy ra được sđ cung nhỏ C D ⏜ = 120 0 và sđ cung lớn C D ⏜ = 240 0
Cho đường tròn (O; R), đường kính AB cố định. Gọi M là trung điểm đoạn OB. Dây CD vuông góc với AB tại M. Điểm E chuyên động trên cung lớn CD (E khác A). Nôi AE cắt CD tại K. Nối BE cắt CD tại H
a, Chứng minh bốn điểm B, M, E, K thuộc một đường tròn
b, Chứng minh AE.AK không đổi
c, Tính theo R diện tích hình quạt tròn giới hạn bởi OB, OC và cung nhỏ BC
Cho đường tròn (O; R), kính AB cố định. Gọi M là trung điểm của OB. Dây CD vuông góc với AB tại M. Điểm E chuyển động trên cung lớn CD. Nối AE cắt CD tại K. Nối BE cắt CD tại H.
a) C/m: AE.AK không đổi
b) Tính theo R diện tích hình quạt tròn giới hạn bởi OB, OC và cung nhỏ BC
c) C/m: tâm I của đường tròn ngoại tiếp tam giác BHK luôn thuộc một đường thẳng cố định.
Cho đương tròn (O;R), đường kính AB cố định. Gọi M là trung điểm của đoạn OB. Dây CD vuông góc AB tại M. Điểm E chuyển độn trên cung lớn CD(E khác A). Nối AE cắt CD tại K. Nối BE cắt CD tại H
a, C/M rằng 4 điểm B,M, E, K thuộc 1 dường tròn
b, C/M AE.AK không đổi
c, Tính theo R diện tích hình quạt tròn giới hạn bởi OB, OC và cung nhỏ BC
Cho(O,R) đường kính AB cố định. Gọi M là trung điểm của OB dây CD vuông góc AB tại M. Điểm E chuyển động trên cung lớn CD(E khác A). Nối AE cắt CD tại K. Nối BE cắt CD tại H
a) CM: BMEK nội tiếp
b) CM: AE nhân AK không đổi
c) Tính theo R diện tích quạt tròn giới hạn bởi OB nhân OC và cung nhỏ BC
d) AD là tiếp tuyến
Cho đường tròn O R; và dây cung BC cố định không đi qua O. A là một điểm di động trên cung lớn BC AB AC sao cho tam giác ABC nhọn. Các đường cao BE CF , cắt nhau tại H . Gọi K là giao điểm của đường thẳng EF và đường thẳng BC . a) Chứng minh tứ giác BCEF nội tiếp, chỉ ra đường kính của đường tròn đó;
b) Chứng minh KB KC KE KF . . . Tính theo R , độ dài cung nhỏ BC và diện tích hình quạt giới hạn bởi bán kính OB OC , và cung nhỏ BC khi góc 0 BAC 60 ; c) Gọi M là giao điểm của AK với đường tròn O ( M khác A). Chứng minh MH vuông góc với AK và MH đi qua trung điểm của BC .Cho đường tròn (O), đường kính AB=2R. Gọi M là trung điểm của OB, đường thẳng d luôn đi qua M cắt (O) tại C và D. Gọi H là trung điểm của CD.
a) Chứng minh H thuộc đường tròn đường kính OM
b) Giả sử CD= R\(\sqrt{3}\), tính độ dài OH theo R và số đo góc COD
c) Gọi I là trực tâm của tam giác ACD. Chứng minh H là trung điểm của BI
Cho đường tròn tâm O bán kính R đường kính MN. Vẽ dây cung AB =R; MA và NB kéo dài cắt nhau tại E a) Tính số đo cung AB nhỏ và số đo của góc MEN b) Gọi H là giao điểm của MB và NA. Chứng minh tứ giác EAHB nội tiếp c) Chứng minh MH.MB+NH.NA = 4R bình phương
Cho (O;R) có 2 đường kính AB và CD vuông góc với nhau. Kẻ dây cung CE qua trung điểm I của OB. Gọi H là hình chiếu vuông góc của A trên dây cung CE. a, Cm: tam giác IHA đồng dạng với tam giác DEC b, tính diện tích tam giác EAC theo R c, tính tỉ số CI.CE/CA.Ca
Cho đường tròn (O;R) đường kính AB . Gọi H là trung điểm OB . Qua H vẽ dây CD vuông góc với AB .Tiếp tuyến tại C và D cắt nhau tại I
cmr 3 điểm O, B , I thẳng hàng