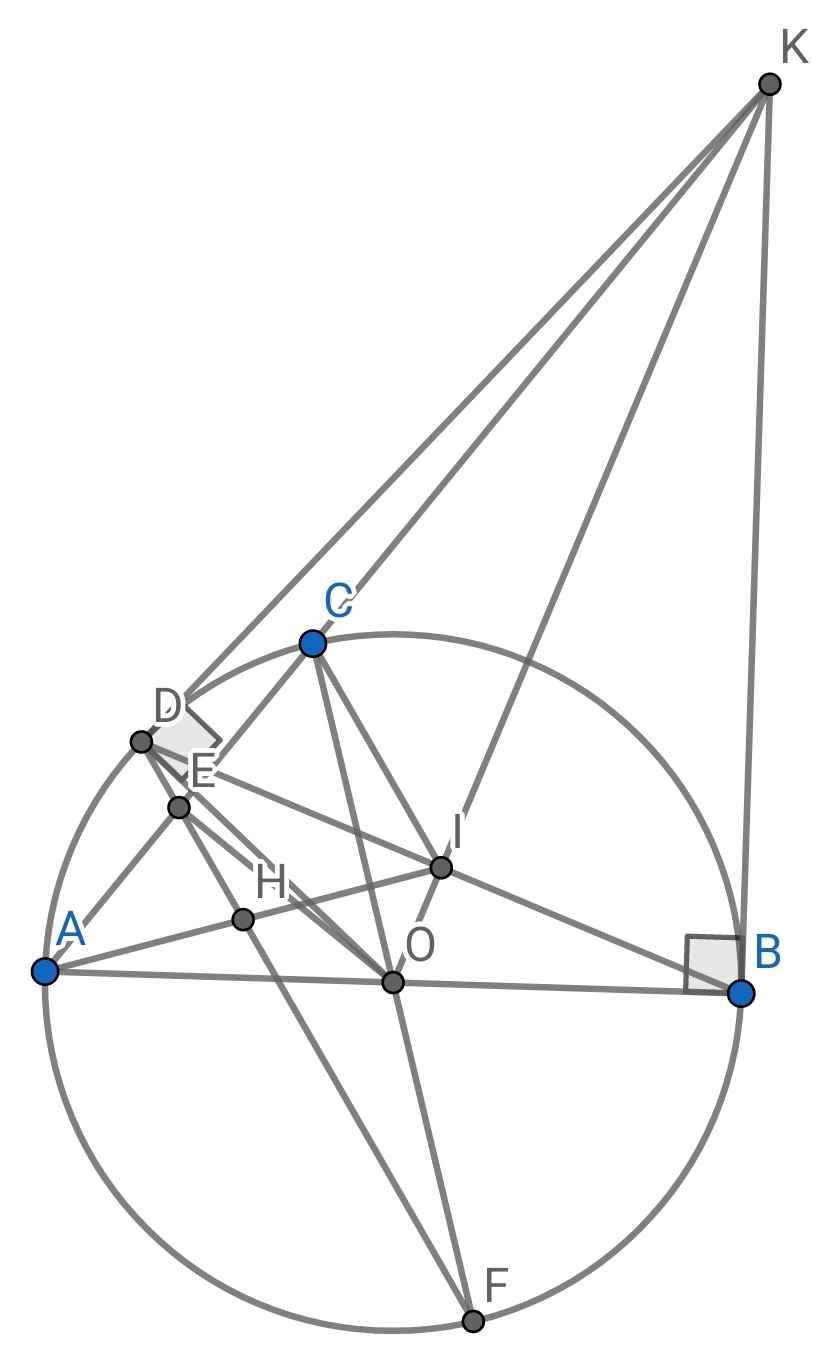
Cho đường tròn (O) đường kính AB, lấy điểm C thuộc (O) (C khác A và B), tiếp tuyến của đường tròn (O) tại B cắt AC ở K. Từ K kẻ tiếp tuyến KD với dường tròn (O) (D là tiếp điểm khác B). a) Chứng minh tứ giác BODK nội tiếp b) Biết OK cắt BD tại I. Chứng minh rằng OI vuông góc với BD c) Gọi E là trung điểm của AC, kẻ dường kính CF của dường tròn (O). FE cắt AI tại H. Chứng minh rằng H là trung điểm của Al.
a) Do BK là tiếp tuyến của (O) tại B (gt)
⇒ ∠OBK = 90⁰
Do DK là tiếp tuyến của (O) tại D (gt)
⇒ ∠ODK = 90⁰
Tứ giác BODK có:
∠OBK = ∠ODK = 90⁰
⇒ ∠OBK + ∠ODK = 180⁰
⇒ BODK nội tiếp (*)
b) Do BK và DK là hai tiếp tuyến cắt nhau tại K
⇒ BK = DK (tính chất hai tiếp tuyến cắt nhau)
⇒ K nằm trên đường trung trực của BD (1)
Lại có:
OB = OD (bán kính)
⇒ O nằm trên đường trung trực của BD (2)
Từ (1) và (2) ⇒ OK là đường trung trực của BD
⇒ OK ⊥ BD
⇒ OI ⊥ BD
c) Xét ∆ODK vuông tại D, đường cao DI
⇒ KD² = KI.KO (3)
Xét ∆KCD và ∆KDA có:
∠K chung
∠KDC = ∠KAD (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung CD)
⇒ ∆KCD ∽ ∆KDA (g-g)
⇒ KD/KA = KC/KD
⇒ KD² = KA.KC (4)
Từ (3) và (4) ⇒ KI.KO = KA.KC
Do E là trung điểm của AC (gt)
⇒ OE ⊥ AC
⇒ ∠OEK = 90⁰
Tứ giác KEOB có:
∠OEK = ∠OBK = 90⁰
⇒ ∠OEK + ∠OBK = 180⁰
⇒ KEOB nội tiếp (**)
Từ (*) và (**) ⇒ K, D, E, O, B cùng nằm trên một đường tròn
Lại có:
KB = KD (cmt)
⇒ ∠DEK = ∠DOK = ∠KOB (các góc nội tiếp chắn các cung bằng nhau trên cùng một đường tròn)
Ta có:
∠DCA = ∠DBA (hai góc nội tiếp cùng chắn cung AD của (O))
Do OK BD tại I (cmt)
⇒ ∆OIB vuông tại I
⇒ ∠KOB + ∠OBI = 90⁰
⇒ ∠DEC + ∠ECD = 90⁰
⇒ ∠EDC = 90⁰
⇒ DE ⊥ DC (5)
Mà ∠FDC = 90⁰ (góc nội tiếp chắn nửa đường tròn)
⇒ FD ⊥ DC (6)
Từ (5) và (6) ⇒ F, H, E, D thẳng hàng
Do KI.KO = KA.KC (cmt)
⇒ KI/KA = KC/KO
Xét ∆KCI và ∆KOA có:
∠K chung
KI/KA = KC/KO (cmt)
⇒ ∆KCI ∽ ∆KOA (c-g-c)
⇒ ∠KCI = ∠KOA (hai góc tương ứng)
Ta có:
∠KEF = ∠KAF + ∠EFA = 90⁰ + ∠EFA (do ∠KEF là góc ngoài của ∆AEF)
⇒ ∠KEF = 90⁰ + ∠DFA = 90⁰ + ∠ABD
∠AOK = ∠OIB + ∠OBI = 90⁰ + ∠OBI (do ∠AOK là góc ngoài của ∆OIB)
⇒ ∠AOK = 90⁰ + ∠ABD
Mà ∠KEF = 90⁰ + ∠ABD (cmt)
⇒ ∠AOK = ∠KEF
Mà ∠AOK = ∠KCI (cmt)
⇒ ∠KCI = ∠KEF
Mà ∠KCI và ∠KEF là hai góc đồng vị
⇒ IC // EF
Mà E là trung điểm của AC (gt)
⇒ H là trung điểm của AI













