Các câu hỏi tương tự
Cho đoạn thẳng CDa) Vẽ ba điểm
N
1
,
N
2
,
N
3
sao cho
C
N
1
D
^
C
N
2
D
^...
Đọc tiếp
Cho đoạn thẳng CD
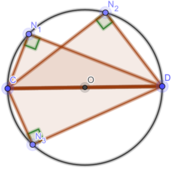
a) Vẽ ba điểm N 1 , N 2 , N 3 sao cho C N 1 D ^ = C N 2 D ^ = C N 3 D ^ = 90 °
b) Chứng minh rằng các điểm N 1 , N 2 , N 3 nằm trên đường tròn đường kính CD.
Cho đoạn thẳng CDVẽ ba điểm
N
1
,
N
2
,
N
3
sao cho
C
N
1
D
^
C
N
2
D
^
C
N
3
D
^...
Đọc tiếp
Cho đoạn thẳng CD
Vẽ ba điểm N 1 , N 2 , N 3 sao cho C N 1 D ^ = C N 2 D ^ = C N 3 D ^ = 90 o
Cho đoạn thẳng CDVẽ ba điểm N1, N2, N3 sao cho
C
N
1
D
^
C
N
2
D
^
C
N
3
D
^
90
o
Đọc tiếp
Cho đoạn thẳng CD
Vẽ ba điểm N1, N2, N3 sao cho C N 1 D ^ = C N 2 D ^ = C N 3 D ^ = 90 o
Cho đoạn thẳng CDVẽ ba điểm N1, N2, N3 sao cho
C
N
1
D
^
C
N
2
D
^
C
N
3
D
^
90
o
Đọc tiếp
Cho đoạn thẳng CD
Vẽ ba điểm N1, N2, N3 sao cho C N 1 D ^ = C N 2 D ^ = C N 3 D ^ = 90 o
cho đương thẳng AB và điểm m bất kỳ trên đoạn thẳng đó .Từ M kẻ tian Mx vuông góc với AB . Trên tia Mx lay điểm C sao cho MC=MA và lấy D sao cho MD=MB (MD>MC) đường tròn tâm O1 đi qua 3 điểm A,M,C và đường tròn tâm O2 đi qua 3 điểm B,M,P 2 đường tròn O1 và O2 cắt nhau tại điểm thứ 2 là N . c/m : 3 điểm A,N,D thẳng hàng va 3 điểm C,N,B thẳng hàng
Bài 5: Cho trước đoạn thẳng AB. Gọi O là trung điểm AB. Trên đoạn AO lấy điểm M tuỳ ý, vẽ nửa đường thẳng qua M và vuông góc với AB, trên nửa đường thẳng này lấy 2 điểm C, D sao cho MA MC và MB MD. Đường thẳng BC cắt đường tròn qua 3 điểm A, M, C tại điểm thứ 2 là N. a) Chứng minh rằng MN luôn đi qua 1 điểm cố định. b) Chứng minh ba điểm A, N, D thẳng hàng.
Đọc tiếp
Bài 5: Cho trước đoạn thẳng AB. Gọi O là trung điểm AB. Trên đoạn AO lấy điểm M tuỳ ý, vẽ nửa đường thẳng qua M và vuông góc với AB, trên nửa đường thẳng này lấy 2 điểm C, D sao cho MA = MC và MB = MD. Đường thẳng BC cắt đường tròn qua 3 điểm A, M, C tại điểm thứ 2 là N.
a) Chứng minh rằng MN luôn đi qua 1 điểm cố định.
b) Chứng minh ba điểm A, N, D thẳng hàng.
Cho đoạn thẳng AC và BD cắt nhau tại trung điểm O của mỗi đoạn. Tên tia AB lấy điểm M sao cho B là trung điểm của AM, trên tia AD lấy điểm N sao cho D là trung điểm của AN. CM 3 điểm M, C, N thẳng hàng.
Cho nửa đường tròn (O), đường kính BC. Gọi D là điểm cố định thuộc đoạn thẳng OC (D khác O và C). Dựng đường thẳng d vuông góc với BC tại điểm D, cắt nửa đường tròn (O) tại điểm A. Trên cung AC lấy điểm M bất kỳ (M khác A và C), tia BM cắt đường thẳng d tại điểm K, tia CM cắt đường thẳng d tại điểm E. Đường thẳng BE cắt nửa đường tròn (O) tại điểm N (N khác B).1. CM: Tứ giác CDNE nội tiếp2. CM: 3 điểm C, K và N thẳng hàng3. Gọi I là tâm đường tròn ngoại tiếp tam giác BKE. Chứng minh rằng điểm I...
Đọc tiếp
Cho nửa đường tròn (O), đường kính BC. Gọi D là điểm cố định thuộc đoạn thẳng OC (D khác O và C). Dựng đường thẳng d vuông góc với BC tại điểm D, cắt nửa đường tròn (O) tại điểm A. Trên cung AC lấy điểm M bất kỳ (M khác A và C), tia BM cắt đường thẳng d tại điểm K, tia CM cắt đường thẳng d tại điểm E. Đường thẳng BE cắt nửa đường tròn (O) tại điểm N (N khác B).
1. CM: Tứ giác CDNE nội tiếp
2. CM: 3 điểm C, K và N thẳng hàng
3. Gọi I là tâm đường tròn ngoại tiếp tam giác BKE. Chứng minh rằng điểm I luôn nằm trên 1 đường thằng cố định khi điểm M thay đổi
Cho nửa đường tròn (O), đường kính BC. Gọi D là điểm cố định thuộc đoạn thẳng OC (D khác O và C). Dựng đường thẳng d vuông góc với BC tại điểm D, cắt nửa đường tròn (O) tại điểm A. Trên cung AC lấy điểm M bất kỳ (M khác A và C), tia BM cắt đường thẳng d tại điểm K, tia CM cắt đường thẳng d tại điểm E. Đường thẳng BE cắt nửa đường tròn (O) tại điểm N (N khác B).1. CM: Tứ giác CDNE nội tiếp2. CM: 3 điểm C, K và N thẳng hàng3. Tiếp tuyến tại N của nửa đường tròn (O) cắt đường thẳng d tại F. CM: F l...
Đọc tiếp
Cho nửa đường tròn (O), đường kính BC. Gọi D là điểm cố định thuộc đoạn thẳng OC (D khác O và C). Dựng đường thẳng d vuông góc với BC tại điểm D, cắt nửa đường tròn (O) tại điểm A. Trên cung AC lấy điểm M bất kỳ (M khác A và C), tia BM cắt đường thẳng d tại điểm K, tia CM cắt đường thẳng d tại điểm E. Đường thẳng BE cắt nửa đường tròn (O) tại điểm N (N khác B).
1. CM: Tứ giác CDNE nội tiếp
2. CM: 3 điểm C, K và N thẳng hàng
3. Tiếp tuyến tại N của nửa đường tròn (O) cắt đường thẳng d tại F. CM: F là trung điểm của KE và OF vuông góc MN
giúp em câu 3 thôi ạ em cảm ơn