Đáp án C
Phương trình có ba nghiệm phân biệt nếu y c t < m < y c d ⇔ - 2 < m < 2
Đáp án C
Phương trình có ba nghiệm phân biệt nếu y c t < m < y c d ⇔ - 2 < m < 2
Cho hàm số y = f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tập tất cả các giá trị của m để đồ thị hàm số y = f x có 5 điểm cực trị là a b ; c với a, b, c là các số nguyên và a b là phân số tối giản. Tính a+b+c
A. 11
B. 8
C. 10
D. 5
Cho đồ thị hàm số y = x 3 + 3 x 2 - 2 có các điểm cực đại A(-2;2) và điểm cực tiểu B(0;-2) thì phương trình x 3 + 3 x 2 - 2 = m có hai nghiệm khi
A. - 2 < m < 2
B. m = - 2 hoặc m = 2
C. m > 2
D. m < - 2
Cho hàm số y = f(x) = a x + b c x + d có đồ thị như hình vẽ bên. Tất cả các giá trị của m để phương trình |f(x)| = m có 2 nghiệm phân biệt là:
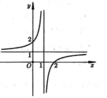
A . m ≥ 2 v à m ≤ 1
B . 0 < m < 1 v à m > 1
C . m > 2 v à m < 1
D . 0 < m < 1
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 x 3 - 3 ( m + 1 ) x 2 + 6 m x có hai điểm cực trị là A và B sao cho đường thẳng AB vuông góc với đường thẳng d : y = x + 2 Số phần tử của S là
A. 0
B. 1
C. 2
D. 3
Cho hàm số y = x 3 - 3 m x 2 + 2 ( m 2 - 1 ) x - m 3 - m (m là tham số). Gọi A, B là hai điểm cực trị của đồ thị hàm số và I(2;-2). Tổng tất cả các giá trị của m để ba điểm I, A, B tạo thành tam giác nội tiếp đường tròn có bán kính bằng 5 là
A. 20 17
B. - 2 17
C. 4 17
D. 14 17
Cho hàm số y = − x + 1 2 x − 1 có đồ thị là (C), đường thẳng d : y = x + m . Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A, B. Gọi k 1 , k 2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A, B. Tìm m để tổng k 1 + k 2 đạt giá trị lớn nhất.
A. m = -1
B. m = -2
C. m = 3
D. m = -5
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d có đồ thị như hình bên. Tất cả các giá trị của m để phương trình | f ( x ) | + m - 1 = 0 có 3 nghiệm phân biệt là
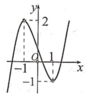
A. m=1
B. m=2
C. m = ± 1
D. m=0
Cho hàm số f ( x ) = a x + b c x + d a , b , c , d ∈ R có đồ thị như hình vẽ bên. Tất cả các giá trị của m để phương trình |f(x)|=m có hai nghiệm phân biệt là
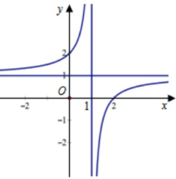
A. m ≥ 2 v à m ≤ 1
B. 0 < m < 1
C. m > 2 và m < 1
D. 0 < m < 1 và m > 1
Để đồ thị hàm số y = - x 4 - ( m - 3 ) x + 2 m + 1 có điểm cực đại mà không có điểm cực tiểu thì tất cả các giá trị thực của tham số m là
A. m ≤ 3
B. m < 3
C. m ≥ 3
D. m > 3