H là trung điểm của MM’, suy ra x M ' + x M = 2 x H
Suy ra
![]()
Tương tự, ta được
![]()
![]()
Vậy 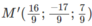

H là trung điểm của MM’, suy ra x M ' + x M = 2 x H
Suy ra
![]()
Tương tự, ta được
![]()
![]()
Vậy 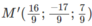
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;-3;1) và đường thẳng d : x + 1 2 = y + 2 − 1 = z 2 . Tìm tọa độ điểm M’ đối xứng với M qua d.
A. M'(3;-3;0)
B. M'(1;-3;2)
C. M'(0;-3;3)
D. M'(-1;-2;0)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;2;3) và đường thẳng d: x = - 1 + t y = 2 + 2 t z = 1 - 2 t . Xác định tọa độ điểm là điểm đối xứng với M qua đường thẳng d.
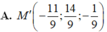
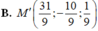
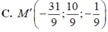
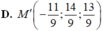
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình lần lượt d: x = 1+2t, y = 2 - t, z = 3t . Tìm tọa độ điểm K đối xứng với điểm I(2;-1;3) qua đường thẳng d
A. K(4;3;3)
B. K(1;-3;3)
C. K(-4;-3;-3)
D. K(-1;3;-3)
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;-1;-6) và hai đường thẳng
d 1 : x - 1 2 = y - 1 - 1 = z + 1 1 , d 2 : x + 2 3 = y + 1 1 = z - 2 2 Đường thẳng đi qua điểm M và cắt cả hai đường thẳng d₁, d₂ tại hai điểm A, B. Độ dài đoạn thẳng AB bằng:
A. √38
B. 2√10
C. 8
D. 12
Cho điểm A(1;0;0) và đường thẳng ∆ : x = 2 + t y = 1 + 2 t z = t Tìm tọa độ điểm A' đối xứng với A qua đường thẳng ∆
Trong không gian Oxyz, cho điểm A(1;0;-1) và đường thẳng d : x - 1 2 = y + 1 2 = z - 1 . Tọa độ điểm A’ đối xứng với A qua đường thẳng d là:
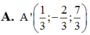
![]()
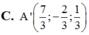
![]()
Trong không gian với hệ toạ độ Oxyz, cho điểm M(2;-3;1) và đường thẳng d : x + 1 2 = y - 2 - 1 = z 2 Tìm toạ độ điểm M 'đối xứng với M qua d
A. M’(3;-3;0)
B. M’(1;-3;2)
C. M’(0;-3;3)
D. M’(-1;-2;0)
Cho điểm M(1; 4; 2) và mặt phẳng (α): x + y + z – 1 = 0 Tìm tọa độ điểm M' đối xứng với M qua mặt phẳng (α).
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2 ; 1 ; 0) và đường thẳng ∆ : x - 1 2 = y + 1 1 = z - 1 . Phương trình tham số của đường thẳng d đi qua M, cắt và vuông góc với Δ là:
A . d : x = 2 + t y = 1 - 4 t z = - 2 t
B . d : x = 2 - t y = 1 + t z = t
C . d : x = 1 + t y = - 1 - 4 t z = 2 t
D . d : x = 2 + 2 t y = 1 + t z = - t