Các câu hỏi tương tự
Cho số phức
z
1
-
2
i
4
-
3
i
-
2
+
8
i
.Cho các phát biểu sau:(1) Modun của z là một số nguyên tốc(2) z có phần thực và phần ảo đều âm(3) z là số thuần thực(4) Số phức liên hợp của z có phần ảo là 3iSố phát biểu sai là: A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Cho số phức z = 1 - 2 i 4 - 3 i - 2 + 8 i .Cho các phát biểu sau:
(1) Modun của z là một số nguyên tốc
(2) z có phần thực và phần ảo đều âm
(3) z là số thuần thực
(4) Số phức liên hợp của z có phần ảo là 3i
Số phát biểu sai là:
A. 1
B. 2
C. 3
D. 4
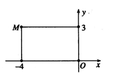
Điểm M trong hình vẽ là điểm biểu diễn của số phức z. Tìm phần thực và phần ảo của số phức. A. Phần thực là -3 và phần ảo là 2. B. Phần thực là 2 và phần ảo là -3. C. Phần thực là -3 và phần ảo là 2i. D. Phần thực là 2 và phần ảo là -3i.
Đọc tiếp
Điểm M trong hình vẽ là điểm biểu diễn của số phức z. Tìm phần thực và phần ảo của số phức.
A. Phần thực là -3 và phần ảo là 2.
B. Phần thực là 2 và phần ảo là -3.
C. Phần thực là -3 và phần ảo là 2i.
D. Phần thực là 2 và phần ảo là -3i.
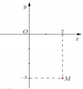
Cho số phức z có điểm biểu diễn là điểm A trong hình vẽ bên. Phần thực và phần ảo của số phức
z
¯
là A. Phần thực bằng 3, phần ảo bằng –2. B. Phần thực bằng 3, phần ảo bằng 2. C. Phần thực bằng 2, phần ảo bằng –3i. D. Phần thực bằng 3, phần ảo bằng 2i.
Đọc tiếp
Cho số phức z có điểm biểu diễn là điểm A trong hình vẽ bên. Phần thực và phần ảo của số phức z ¯ là
A. Phần thực bằng 3, phần ảo bằng –2.
B. Phần thực bằng 3, phần ảo bằng 2.
C. Phần thực bằng 2, phần ảo bằng –3i.
D. Phần thực bằng 3, phần ảo bằng 2i.
Cho số phức z = 3 - 4 i . Phần thực và phần ảo số phức z là
A. Phần thực bằng 3 và phần ảo bằng -4i
B. Phần thực bằng 3 và phần ảo bằng 4.
C. Phần thực bằng 3 và phần ảo bằng 4i
D. Phần thực bằng 3 và phần ảo bằng -4.
Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z. Tìm phần thực và phần ảo của số phức z A. Phần thực là -4 và phần ảo là 3 B. Phần thực là 3 và phần ảo là -4i C. Phần thực là 3 và phần ảo là -4 D. Phần thực là -4 và phần ảo là 3i
Đọc tiếp
Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z. Tìm phần thực và phần ảo của số phức z
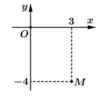
A. Phần thực là -4 và phần ảo là 3
B. Phần thực là 3 và phần ảo là -4i
C. Phần thực là 3 và phần ảo là -4
D. Phần thực là -4 và phần ảo là 3i
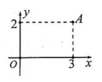
Điểm A trong hình vẽ bên là điểm biểu diễn của số phức z. Tìm phần thực và phần ảo của số phức
z
-
A. Phần thực là -3 và phần ảo là 2. B. Phần thực là -3 và phần ảo là 2i. C. Phần thực là 3 và phần ảo là -2. D. Phần thực là 3 và phần ảo là -2i.
Đọc tiếp
Điểm A trong hình vẽ bên là điểm biểu diễn của số phức z. Tìm phần thực và phần ảo của số phức z -
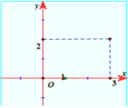
A. Phần thực là -3 và phần ảo là 2.
B. Phần thực là -3 và phần ảo là 2i.
C. Phần thực là 3 và phần ảo là -2.
D. Phần thực là 3 và phần ảo là -2i.
Điểm A trong hình vẽ bên là điểm biểu diễn của số phức z. Tìm phần thực và phần ảo của số phức z. A. Phần thực bằng 3 và phần ảo bằng 2. B. Phần thực bằng 3 và phần ảo bằng -2. C. Phần thực bằng 3 và phần ảo bằng 2i. D. Phần thực bằng 3 và phần ảo bằng -2i.
Đọc tiếp
Điểm A trong hình vẽ bên là điểm biểu diễn của số phức z. Tìm phần thực và phần ảo của số phức z.
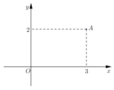
A. Phần thực bằng 3 và phần ảo bằng 2.
B. Phần thực bằng 3 và phần ảo bằng -2.
C. Phần thực bằng 3 và phần ảo bằng 2i.
D. Phần thực bằng 3 và phần ảo bằng -2i.
Phần thực và phần ảo của số phức z=3+4i lần lượt là
A. 3; 4i
B. 3i; 4
C. 3; 4
D. 4; 3
Điểm A trong hình vẽ bên là điểm biểu diễn của số phức z.Tìm phần thực và phần ảo của số phức
z
¯
. A. Phần thực bằng 3 và phần ảo bằng 2. B. Phần thực bằng 3 và phần ảo bằng
-
2
. C. Phần thực bằng 3 và phần ảo bằng 2i. D. Phần thực bằng 3 và phần ảo bằng
-
2
i
.
Đọc tiếp
Điểm A trong hình vẽ bên là điểm biểu diễn của số phức z.Tìm phần thực và phần ảo của số phức z ¯
.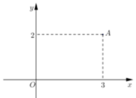
A. Phần thực bằng 3 và phần ảo bằng 2.
B. Phần thực bằng 3 và phần ảo bằng - 2 .
C. Phần thực bằng 3 và phần ảo bằng 2i.
D. Phần thực bằng 3 và phần ảo bằng - 2 i .