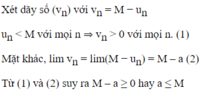Các câu hỏi tương tự
Cho dãy số
(
u
n
)
thoả mãn điều kiện: Với mọi
n
∈
N
∗
thì
0
u
n
1
v
à
u
n
+
1
1
-
1...
Đọc tiếp
Cho dãy số ( u n ) thoả mãn điều kiện: Với mọi n ∈ N ∗ thì 0 < u n < 1 v à u n + 1 < 1 - 1 4 u n Chứng minh dãy số đã cho là dãy giảm.
Cho dãy số (U n) với U n = 2n/ n^2 + 1 , ∀ n ∈ N*
a) Viết 5 số hạng đầu
b) số 9/U¹ là hạng thứ mấy
c) chứng minh dãy số bị giảm và bị chặn
Cho dãy số (U n) với U n = 2n/ n^2 + 1 , ∀ n ∈ N*
a) Viết 5 số hạng đầu
b) số 9/U¹ là hạng thứ mấy
c) chứng minh dãy số bị giảm và bị chặn
Cho dãy số
u
(
n
)
xác định bởi
u
(
1
)
1
;
u
(
m
+
n
)
u...
Đọc tiếp
Cho dãy số u ( n ) xác định bởi u ( 1 ) = 1 ; u ( m + n ) = u ( m ) + u ( n ) + m n , ∀ m , n ∈ ℕ * . Tính u ( 2017 )
A. 2035153
B. 2035154
C. 2035155
D. 2035156
Dãy số (��)(u
n) thỏa mãn ��≥�2u
≥n22 với mọi n. Tính lim un
.
Đọc tiếp
Dãy số thỏa mãn với mọi . Tính lim un
.
Cho tam giác ABC, điểm I thoả mãn:
5
M
A
→
2
M
B
→
. Nếu
I
A
→
m
I
M
→
+
n...
Đọc tiếp
Cho tam giác ABC, điểm I thoả mãn: 5 M A → = 2 M B → . Nếu I A → = m I M → + n I B → thì cặp số (m; n) bằng:
A. 
B. 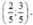
C. 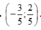
D. 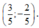
Cho hai dãy số
(
u
n
)
và
(
v
n
)
. Chứng minh rằng nếu lim
v
n
0
v
à
|
u
n
|
≥
v
n
với mọi n thì
l
i
m
...
Đọc tiếp
Cho hai dãy số ( u n ) và ( v n ) . Chứng minh rằng nếu lim v n = 0 v à | u n | ≥ v n với mọi n thì l i m u n = 0
Biết dãy số
u
n
thỏa mãn
u
n
-
1
1
3
với mọi n. Chứng minh rằng:
l
i
m
u
n
...
Đọc tiếp
Biết dãy số u n thỏa mãn u n - 1 < 1 3 với mọi n. Chứng minh rằng: l i m u n = 1 .
Chứng minh dãy số (un) với \(u_n=\sqrt{n^2+2}-n\) là dãy số giảm và bị chặn