Đặt vn = un – 1.
Lấy số dương d > 0 bé tùy ý
⇒ luôn tồn tại 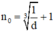 thỏa mãn
thỏa mãn 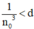
⇒ 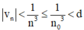 với mọi n ≥ n0.
với mọi n ≥ n0.
⇒ Theo định nghĩa ta có:
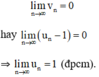
Đặt vn = un – 1.
Lấy số dương d > 0 bé tùy ý
⇒ luôn tồn tại 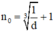 thỏa mãn
thỏa mãn 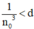
⇒ 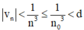 với mọi n ≥ n0.
với mọi n ≥ n0.
⇒ Theo định nghĩa ta có:
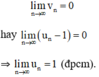
Dãy số thỏa mãn với mọi . Tính lim un
.
Cho dãy số ( u n ) thoả mãn điều kiện: Với mọi n ∈ N ∗ thì 0 < u n < 1 v à u n + 1 < 1 - 1 4 u n Chứng minh dãy số đã cho là dãy giảm.
Cho dãy số ( u n ) thoả mãn u n > M với mọi n. Chứng minh rằng nếu l i m u n = a thì a ≤ M
Cho dãy số u ( n ) xác định bởi u ( 1 ) = 1 ; u ( m + n ) = u ( m ) + u ( n ) + m n , ∀ m , n ∈ ℕ * . Tính u ( 2017 )
A. 2035153
B. 2035154
C. 2035155
D. 2035156
Cho dãy số ( u n ) xác định bởi u 1 = 1 u n + 1 = 2 u n + 3 u n + 2 v ớ i n ≥ 1
a) Chứng minh rằng u n > 0 với mọi n.
b) Biết ( u n ) có giới hạn hữu hạn. Tìm giới hạn đó.
Cho dãy số (Un) xác định bởi U1=-3 và U(n+1)=Un+ n^2 -3n +4, mọi n thuộc N*. Số 1391 là số hạng thứ mấy của dãy ?
Cho dãy số (un) thỏa mãn ln2u6 – ln u6 = ln u4 – 1 và un+1 = un.e với mọi n ≥ 1 Tìm u1
A. e
B. e2
C. e-3
D. e-4