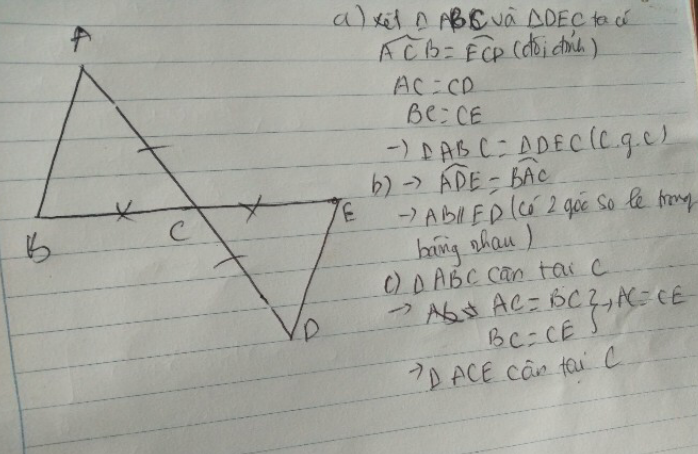Các câu hỏi tương tự
Cho ΔABC , AB=AC , phân giác AD .
a, Chứng minh : ΔABD=ΔACD
b, Vẽ trung tuyến CF , G là giao điểm CF và AD . Chứng minh G là trọng tâm ΔABC
c, Gọi H là trung điểm của CD . Đường thẳng \(\perp\)CD tại H cắt AC tại E . Chứng minh : ΔDEC cân
d, So sánh AD và BD
Bài 6: Cho ∠xAy, lấy điểm B trên tia Ax, điểm D trên tia Ay sao cho AB AD. Trên tia Bx lấy điểm E, trên tia Dy lấy điểm C sao cho BE DC. Chứng minh ΔABC ΔADE.Bài 7: Cho đoạn thẳng AB có M là trung điểm. Qua M kẻ đường thẳng d vuông góc với AB. Lấy C ∈ d (C khác M). Chứng minh CM là tia phân giác của ∠ACB.Bài 8: Cho ΔABC có AB AC, phân giác AM (M ∈ BC).Chứng minh: a) ΔABM ΔACM. b) M là trung điểm của BC và AM ⊥ BC.Bài 9: Cho ΔABC, trên nửa mặt phẳng bờ AC không chứa điểm B, lấy điểm D sao ch...
Đọc tiếp
Bài 6: Cho ∠xAy, lấy điểm B trên tia Ax, điểm D trên tia Ay sao cho AB = AD. Trên tia Bx lấy điểm E, trên tia Dy lấy điểm C sao cho BE = DC. Chứng minh ΔABC = ΔADE.
Bài 7: Cho đoạn thẳng AB có M là trung điểm. Qua M kẻ đường thẳng d vuông góc với AB. Lấy C ∈ d (C khác M). Chứng minh CM là tia phân giác của ∠ACB.
Bài 8: Cho ΔABC có AB = AC, phân giác AM (M ∈ BC).
Chứng minh: a) ΔABM = ΔACM. b) M là trung điểm của BC và AM ⊥ BC.
Bài 9: Cho ΔABC, trên nửa mặt phẳng bờ AC không chứa điểm B, lấy điểm D sao cho AD // BC và AD = BC. Chứng minh: a) ΔABC = ΔCDA. b) AB // CD và ΔABD = ΔCDB.
Bài 10: Cho ΔABC có ∠A = 90 độ, trên cạnh BC lấy điểm E sao cho BA = BE. Tia phân giác ∠B cắt AC ở D.
a) Chứng minh: ΔABD = ΔEBD. b) Chứng minh: DA = DE. c) Tính số đo ∠BED.
Bài 11: Cho ΔABD, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh: a) ΔABM = ΔECM. b) AB = CE và AC // BE.
(* Chú ý: Δ là tam giác, ∠ là góc, ⊥ là vuông góc, // là song song.)
Cho ΔABC cân tại A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho: AD = AE
a) Chứng minh: ΔADC = ΔAEB
b) Gọi I là giao điểm của CD và BE. Chứng minh: ΔIBC là tam giác cân
Cho ΔABC vuông tại A có AB = 5cm, AC = 12cm.
a) Tính BC.
b) Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Chứng minh ΔABC = ΔADC.
c) Đường thẳng qua A song song với BC cắt CD tại E. Chứng minh ΔEAC cân.
d) Gọi F là trung điểm của BC. Chứng minh rằng CA, DF, BE đồng quy tại một điểm
Cho ΔABC vuông tại A có AB = 5cm, AC = 12cm.
a. Tính BC.
b. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Chứng minh ΔABC = ΔADC.
c. Đường thẳng qua A song song với BC cắt CD tại E. Chứng minh ΔEAC cân.
d. Gọi F là trung điểm của BC. Chứng minh rằng CA, DF, BE đồng quy tại một điểm.
làm mỗi ý d thui cx đc
cho Δabc cân tại A. Điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho AD=AE. Gọi K là giao điểm BE và CD. Chứng minh
a, BE=AE
b,ΔKBD=ΔKCE
c,AK là phân giác ∠a
d,ΔKBC cân
Cho ΔABC vuông cân tại đỉnh A, M là trung điểm của BC. Trên cạnh BC lấy điểm D tuỳ ý (D khác M). Từ B,C hạ BE, CF vuông góc với AD. Chứng minh:
a) ΔAEB = ΔAFC
b) ΔAME = ΔCMF
c) ΔMEF vuông cân.
Cho ΔABC có ∠A= 90o90o, đường phân giác xuất phát từ B cắt AC tại D. Qua D kẻ đường thẳng d vuông góc với BC tại E và cắt AB tại F. CM:
a) ΔABC là tam giác cân
b) BD là đường trung tuyến của ΔFBC
c) BD + FD < BC + FC
d) ΔABC có thêm điều kiện gì về góc để D là điểm cách đều ba cạnh của ΔFBC? Vì sao? Vẽ hình minh họa
Cho ΔABC vuông tại A (AB < AC). Trên tia đối của tia AB, lấy điểm D sao cho AB = AD.
a) Chứng minh ΔACB = ΔACD, từ đó suy ra ΔBCD cân
b) Gọi E, F lần lượt là trung điểm của CD và BC, BE cắt CA tại I. Chứng minh D, I, F thẳng hàng
c) Kẻ đường thẳng qua D, song song BC và cắt BE tại M. Gọi G là giao điểm của MA và CD. Chứng minh BC = 6GE