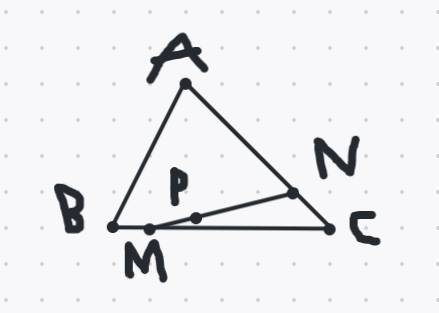
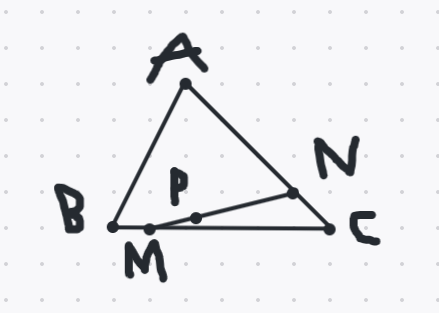
a/ Ta có
\(BC=5xBM\Rightarrow BM=\dfrac{1}{5}xBC\Rightarrow CM=BC-BM=BC-\dfrac{1}{5}xBC=\dfrac{4}{5}xBC\)
\(AN=\dfrac{3}{4}xAC\Rightarrow CN=AC-AN=AC-\dfrac{3}{4}xAC=\dfrac{1}{4}xAC\)
Hai tg AMC và tg ABC có chungg đường cao từ A->BC nên
\(\dfrac{S_{AMC}}{S_{ABC}}=\dfrac{CM}{BC}=\dfrac{4}{5}\Rightarrow S_{AMC}=\dfrac{4}{5}xS_{ABC}\)
Hai tg ACM và tg MNC có chung đường cao từ M->AC nên
\(\dfrac{S_{MNC}}{S_{AMC}}=\dfrac{CN}{AC}=\dfrac{1}{4}\Rightarrow S_{MNC}=\dfrac{1}{4}xS_{AMC}=\dfrac{1}{4}x\dfrac{4}{5}xS_{ABC}=\dfrac{1}{5}xS_{ABC}=\dfrac{1}{5}x35=7cm^2\)
b/
\(S_{AMN}=S_{AMC}-S_{MNC}=\dfrac{4}{5}xS_{ABC}-\dfrac{1}{5}xS_{ABC}=\dfrac{3}{5}xS_{ABC}\)
Ta có
\(NP=\dfrac{2}{3}xNM\Rightarrow MP=NM-NP=NM-\dfrac{2}{3}xNM=\dfrac{1}{3}xNM\)
Hai tg AMP và tg AMN có chung đường cao từ A->NM nên
\(\dfrac{S_{AMP}}{S_{AMN}}=\dfrac{MP}{NM}=\dfrac{1}{3}\Rightarrow S_{AMP}=\dfrac{1}{3}xS_{AMN}=\dfrac{1}{3}x\dfrac{3}{5}xS_{ABC}=\dfrac{1}{5}xS_{ABC}\)
Ta có
\(S_{ABM}=S_{ABC}-S_{ACM}=S_{ABC}-\dfrac{4}{5}xS_{ABC}=\dfrac{1}{5}xS_{ABC}\)
\(\Rightarrow S_{AMP}=S_{ABM}\)