Các câu hỏi tương tự
Cho hàm số
f
(
x
)
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
,
(
a
,
b
,
c
,
d
,
e
∈
ℝ
)
Hàm yf(x) có bảng xét dấu như sau: Số nghiệm của phương trình f(x)e là A....
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e , ( a , b , c , d , e ∈ ℝ ) Hàm y=f'(x) có bảng xét dấu như sau:
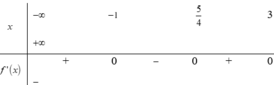
Số nghiệm của phương trình f(x)=e là
A. 1
B. 0
C. 2
D. 3
Cho hàm số
f
(
x
)
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
có bảng biến thiên như hình vẽ sauCó bao nhiêu số nguyên dương m để hàm số y|f(x)+m| có 7 điểm cực trị. A. 0. B. 21. C. 18. D. 19.
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e có bảng biến thiên như hình vẽ sau
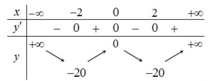
Có bao nhiêu số nguyên dương m để hàm số y=|f(x)+m| có 7 điểm cực trị.
A. 0.
B. 21.
C. 18.
D. 19.
Biết rằng đồ thị hàm số
y
f
t
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
,
a
,
b
,
c
,
d
∈...
Đọc tiếp
Biết rằng đồ thị hàm số y = f t = a x 4 + b x 3 + c x 2 + d x + e , a , b , c , d ∈ ℝ ; a ≠ 0 , b ≠ 0 cắt trục hoành Ox tại 4 điểm phân biệt. Khi đó đồ thị hàm số y = g x = 4 a x 3 + 3 b x 2 + 2 c x + d 2 - 2 6 a x 2 + 3 b x + c . a x 4 + b x 3 + c x 2 + d x + e cắt trục hoành Ox tại bao nhiêu điểm?
A. 6
B. 0
C. 4
D. 2
Biết rằng đồ thị hàm số
y
f
x
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+...
Đọc tiếp
Biết rằng đồ thị hàm số y = f x = a x 4 + b x 3 + c x 2 + d x + e a , b , c , d , e ∈ ℝ ; a ≠ 0 ; b ≠ 0 cắt trục hoành tại 4 điểm phân biệt. Khi đó đồ thị hàm số y = g x = 4 a x 3 + 3 b x 2 + 2 c x + d 2 - 2 6 a x 2 + 3 b x + c a x 4 + b x 3 + c x 2 + d x + e cắt trục hoành Ox tại bao nhiêu điểm?
A. 6.
B. 0.
C. 4.
D. 2.
Hình vẽ bên là đồ thị của hàm số
f
(
x
)
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
Phương trình f(x)+m0 có bốn nghiệm thực phân biệt khi và chỉ khi A.
m
∈
(
-
1
;
0
)
B. ...
Đọc tiếp
Hình vẽ bên là đồ thị của hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e Phương trình f(x)+m=0 có bốn nghiệm thực phân biệt khi và chỉ khi
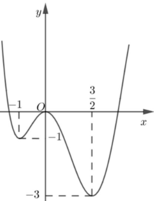
A. m ∈ ( - 1 ; 0 )
B. m ∈ ( - 3 ; 0 )
C. m ∈ ( 0 ; 1 )
D. m ∈ 1 ; 3
Cho hàm số
f
x
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
m
(với
a
,
b
,
c
,
d
,
m
∈
ℝ
). Hàm số
y
f
x
có đồ thị như hình...
Đọc tiếp
Cho hàm số f x = a x 4 + b x 3 + c x 2 + d x + m (với a , b , c , d , m ∈ ℝ ). Hàm số y = f ' x có đồ thị như hình vẽ bên. Tập nghiệm của phương trình f x = m có số phần tử là
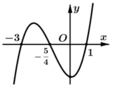
A. 1
B. 2
C. 3
D. 4
Cho hàm số
f
x
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
.
Hàm số
y
f
x
có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng? A. a + c 0 B.
a
+
b
+...
Đọc tiếp
Cho hàm số f x = a x 4 + b x 3 + c x 2 + d x + e . Hàm số y = f ' x có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
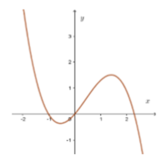
A. a + c > 0
B. a + b + c + d < 0
C. a + c < b + d
D. b + d - c > 0
Cho đa thức: P(x) = ax4 + bx3 + cx2 + dx + e nguyên với mọi x
C/M : a, b, c, d, e nguyên
Biết rằng phương trình
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
0
a
,
b
,
d
,
e
∈
ℝ
,...
Đọc tiếp
Biết rằng phương trình a x 4 + b x 3 + c x 2 + d x + e = 0 a , b , d , e ∈ ℝ , a ≠ 0 , b ≠ 0 có 4 nghiệm thực phân biệt. Hỏi phương trình sau có bao nhiêu nghiệm thực?
4
a
x
3
+
3
b
x
2
+
2
c
x
+
d
2
−
2
6
a
x
2
+
3
b
x
+
c
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
=
0
A. 0
B. 2
C. 4
D. 6


