Các câu hỏi tương tự
Cho đa giác đều 2n đỉnh
n
≥
2
.
Hỏi có bao nhiêu hình chữ nhật có 4 đỉnh là 4 trong 2n đỉnh của đa giác. A.
C
2
n
2
B.
C
n
4
C.
C
2
n
4
D. ...
Đọc tiếp
Cho đa giác đều 2n đỉnh n ≥ 2 . Hỏi có bao nhiêu hình chữ nhật có 4 đỉnh là 4 trong 2n đỉnh của đa giác.
A. C 2 n 2
B. C n 4
C. C 2 n 4
D. C n 2
Cho một đa giác đều 2n đỉnh Tìm n biết số hình chữ nhật được tạo ra từ bốn đỉnh trong số 2n đỉnh của đa giác đó là 45 A. n 12 B. n 10 C. n 9 D. n 45
Đọc tiếp
Cho một đa giác đều 2n đỉnh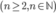 
Tìm n biết số hình chữ nhật được tạo ra từ bốn đỉnh trong số 2n đỉnh của đa giác đó là 45
A. n = 12
B. n = 10
C. n = 9
D. n = 45
Cho (H) là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O . Gọi S là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn một tam giác vuông trong tập S là
3
29
. Tìm n? A. 20 B. 12 C. 15 D. 10
Đọc tiếp
Cho (H) là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O 
. Gọi S là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn một tam giác vuông trong tập S là
3
29
. Tìm n?
A. 20
B. 12
C. 15
D. 10
Cho một đa giác đều gồm 2n đỉnh
n
≥
2
,
n
∈
ℕ
.
Chọn ngẫu nhiên ba đỉnh trong số 2n đỉnh của đa giác, xác suất ba đỉnh được chọn tạo thành một tam giác vuông là 1/5. Tìm n . A. 5 B. 4 C. 10 D. 8
Đọc tiếp
Cho một đa giác đều gồm 2n đỉnh n ≥ 2 , n ∈ ℕ . Chọn ngẫu nhiên ba đỉnh trong số 2n đỉnh của đa giác, xác suất ba đỉnh được chọn tạo thành một tam giác vuông là 1/5. Tìm n .
A. 5
B. 4
C. 10
D. 8
Cho đa giác đều
A
1
A
2
A
3
.
.
.
A
30
nội tiếp trong đường tròn (O). Tính số hình chữ nhật có các đỉnh là 4 trong 30 đỉnh của đa giác đó. A. 105 B. 27405 C. 27406 D. 106
Đọc tiếp
Cho đa giác đều A 1 A 2 A 3 . . . A 30 nội tiếp trong đường tròn (O). Tính số hình chữ nhật có các đỉnh là 4 trong 30 đỉnh của đa giác đó.
A. 105
B. 27405
C. 27406
D. 106
Cho tập A gồm n điểm phân biệt không có 3 điểm nào thẳng hàng. Tìm n biết rằng số tam giác mà 3 đỉnh thuộc A gấp đôi số đoạn thẳng được nối từ 2 điểm thuộc A.
A. n = 6.
B. n = 12.
C. n = 8.
D. n =15.
Cho một đa giác đều gồm 2n đỉnh (n≥2, nÎN*). Chọn ngẫu nhiên ba đỉnh trong sổ 2n đỉnh của đa giác, xác suất ba đỉnh được chọn tạo thành một tam giác vuông là 1 5 . Tìm n.
A. 5
B. 4
C. 10
D. 8
Cho một đa giác đều 20 đỉnh nội tiếp trong đường tròn O. Chọn ngẫu nhiên 4 đỉnh của đa giác đó. Tính xác suất sao cho 4 đỉnh được chọn là 4 đỉnh của một hình chữ nhật
A. 3 323
B. 4 9
C. 2 969
D. 7 216
Gọi là đa giác đều 4n đỉnh nội tiếp trong đường tròn tâm O(nϵ ℕ*) và X là tập hợp các tam giác có ba đỉnh là các đỉnh của đa giác. Chọn ngẫu nhiên một tam giác thuộc tập X. Biết rằng xác suất chọn được một tam giác vuông thuộc tập X là 1/13. Giá trị của n là A. 9. B. 14. C. 10. D. 12.
Đọc tiếp
Gọi là đa giác đều 4n đỉnh nội tiếp trong đường tròn tâm O(nϵ ℕ*) và X là tập hợp các tam giác có ba đỉnh là các đỉnh của đa giác. Chọn ngẫu nhiên một tam giác thuộc tập X. Biết rằng xác suất chọn được một tam giác vuông thuộc tập X là 1/13. Giá trị của n là
A. 9.
B. 14.
C. 10.
D. 12.