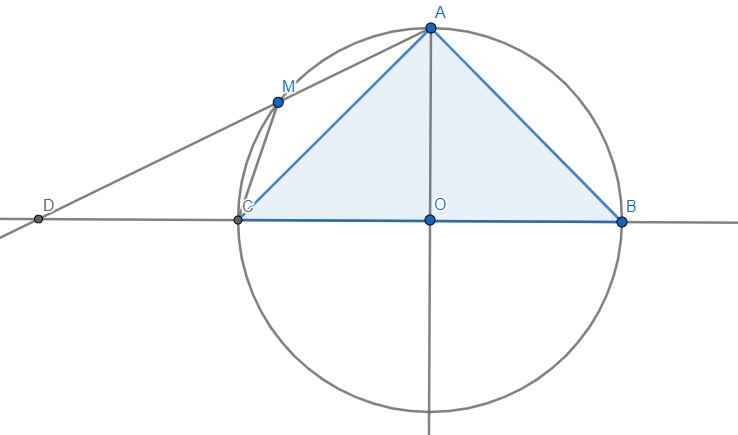
1) Kẻ OC
Vì \(\Delta ABC\) cân tại A \(\Rightarrow\) OA là trung trực \(\Delta\) ABC
Xét \(\Delta\)OAC có:
\(AC^2=\left(R\sqrt{2}\right)^2=2R^2\)
\(OA^2+OC^2=R^2+R^2=2R^2\)
\(\Rightarrow\Delta\) OAC vuông cân tại O
\(\Rightarrow\widehat{AOC}=90^o\)
Tương tự có: \(\Rightarrow\widehat{AOB}=90^o\)
\(\Rightarrow\widehat{AOC}+\widehat{AOB}=90^o+90^o=180^o\)
\(\Rightarrow\)B,O,C thẳng hàng
mà OA là trung trực \(\Rightarrow OB=OC=\dfrac{BC}{2}\)
lại có \(OC=R\Rightarrow BC=2R\)
2) Vì \(\Delta\)ABC cân tại A\(\Rightarrow AB=AC\Rightarrow\stackrel\frown{AB}=\stackrel\frown{AC}\Rightarrow sđ\stackrel\frown{AB}=sđ\stackrel\frown{AC}\)
Kẻ MC
Xét (O) có:
\(\widehat{MCA}=\dfrac{1}{2}sđ\stackrel\frown{MA}\) (góc nt chắn \(\stackrel\frown{MA}\) )
\(\widehat{ADC}=\dfrac{1}{2}\left(sđ\stackrel\frown{AB}-sđ\stackrel\frown{MC}\right)\) (góc có đỉnh ngoài đường tròn)
\(\Rightarrow\widehat{ADC}=\dfrac{1}{2}\left(sđ\stackrel\frown{AC}-sđ\stackrel\frown{MC}\right)\)
\(\Rightarrow\widehat{ADC}=\dfrac{1}{2}sđ\stackrel\frown{MA}\)
\(\Rightarrow\widehat{MCA}=\widehat{ADC}\)
Xét \(\Delta\) AMC và \(\Delta\) ACD có:
\(\widehat{MAC}\) chung
\(\widehat{MCA}=\widehat{ADC}\)
\(\Rightarrow\Delta AMC\sim\Delta ACD\)
\(\Rightarrow\dfrac{AM}{AC}=\dfrac{AC}{AD}\Rightarrow AC^2=AM\cdot AD\) (đpcm)