Đáp án C.
Gọi số hạng đầu và công sai của CSC (un) là u1, d ta có
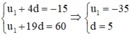
Suy ra ![]()
Đáp án C.
Gọi số hạng đầu và công sai của CSC (un) là u1, d ta có
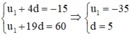
Suy ra ![]()
Cho cấp số cộng u n có u 5 = - 15 , u 20 = 60 . Tổng S 20 của 20 số hạng đầu tiên của cấp số cộng là
A. S 20 = 600
B. S 20 = 60
C. S 20 = 250
D. S 20 = 500
Cho cấp số cộng (Un) có u 5 = - 15 , u 20 = 60 . Tổng của 10 số hạng đầu tiên của cấp số cộng này là
A. S 10 = - 125
B. S 10 = - 250
C. S 10 = 200
D. S 10 = - 200
Cho cấp số cộng (un) có u 5 = - 15 ; u 20 = 60 Tổng của 10 số hạng đầu tiên của (un) bằng
A. S10 = -125
B. S10 = -250
C. S10 = 200
D. S10 = -200
Cho cấp số cộng có u 5 = - 15 ; u 20 = 60 . Tổng của 20 số hạng đầu tiên của cấp số cộng trên là
A. 200
B. 250
C. -230
D. -250
Cho cấp số cộng ( u n ) biết u 5 = 18 v à 4 S n = S 2 n . Tìm số hạng đầu tiên u 1 và công sai d của cấp số cộng
A. u 1 = 2 , d = 4
B. u 1 = 2 , d = 3
C. u 1 = 2 , d = 2
D. u 1 = 3 , d = 2
Cho cấp số cộng u n biết u 5 = 18 và 4 S n = S 2 n . Tìm số hạng đầu tiên u 1 và công sai d của cấp số cộng.
A. u 1 = 2 , d = 4
B. u 1 = 2 , d = 3
C. u 1 = 2 , d = 2
D. u 1 = 3 , d = 2
Cho cấp số cộng u n thoả mãn u 5 + 3 u 3 − u 2 = − 21 3 u 7 − 2 u 4 = − 34 . Tổng 15 số hạng đầu của cấp số cộng là
A. -244
B. -274
C. -253
D. -285
Cho cấp số cộng u n với số hạng đầu u 1 = 2 và số hạng thứ năm u 5 = 14 . Tổng của 10 số hạng đầu của cấp số cộng u n là
A. 232
B. 126
C. 155
D. 187
Gọi S n = 4 n + 7 n + 10 n + ... + 1 + 3 n n . Khi đó S 20 có giá trị là
A. 34
B. 30,5
C. 325
D. 32,5