Đáp án A.
Đặt ![]() ,
,
khi đó ![]() và
và ![]()
Nên ta có
![]()
![]()
Khi đó
![]()
![]()
Dễ thấy
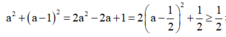
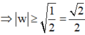
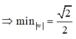
Đáp án A.
Đặt ![]() ,
,
khi đó ![]() và
và ![]()
Nên ta có
![]()
![]()
Khi đó
![]()
![]()
Dễ thấy
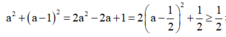
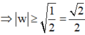
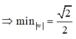
Cho số phức z thỏa mãn (3 + 2i)z + (2 - i)2 = 4 + i. Môđun của số phức w = ( z + 1 ) z là
A. 2
B. 4
C. 10
D. 10
Cho số phức z thỏa mãn ( 2 + i ) z + 2 ( 1 + 2 i ) 1 + i . Môđun của số phức w = z + i + 1 là
A. 3
B. 4
C. 5
D. 6
Cho số phức z thỏa mãn 5 ( z + i ) z + 1 = 2 - i . Khi đó môđun của số phức w = 1 + z + z 2 là
A. 5
B. 13
C. 13
D. 5
Cho số phức z thỏa mãn | z + 1 - i | = | z | . Giá trị nhỏ nhất của môđun của z là
A. 0
B. 1 2
C. 1
D. 1 2
Cho z = x + y i với x, y ∈ R là số phức thỏa mãn điều kiện z ¯ + 2 - 3 i ≤ | z + i - 2 | ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 x . Tính M+m.
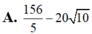
![]()
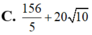
![]()
Tìm số phức z thỏa mãn | z - 1 - i | = 5 và biểu thức T = | z - 7 - 9 i | + 2 | z - 8 i | đạt giá trị nhỏ nhất
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn z - 2 - 3 i = 1 . Tìm giá trị lớn nhất của z
A. 2 + 13
B. 13 - 1
C. 13
D. 1 + 13
Trong các số phức thỏa mãn điều kiện z - 4 i - 2 = 2 i - z , môđun nhỏ nhất của số phức z bằng:
A. 2
B. 3
C. 2 2
D. 2 3
Cho số phức z thỏa mãn (1 + i)(z - i) + 2z = 2i. Môđun của số phức: w = z - 2 z + 1 z 2 là
A. 2
B. 4
C. 10
D. 10