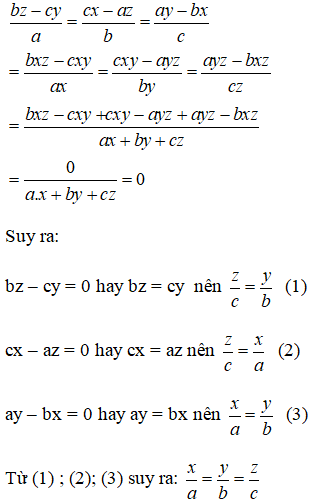2 tháng 4 2022 lúc 19:37
Các câu hỏi tương tự
10 tháng 9 2023 lúc 11:17
\(\dfrac{bz-cy}{z}=\dfrac{cx-az}{b}=\dfrac{ay-bx}{c}\) (1) CMR: \(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\) (*)
Cho các số a, b, c, x, y, z Thỏa mãn điều kiện: \(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\).Chứng minh rằng:
\(\dfrac{bz-cy}{a}=\dfrac{cx-az}{b}=\dfrac{ay-bx}{c}\)
Cho biết : \(\dfrac{bz-cy}{a}=\dfrac{cx-az}{b}=\dfrac{ay-bx}{c}\) với a,b,c \(\ne\) 0
Chứng minh rằng \(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\)
cho \(\dfrac{cy-bz}{x}=\dfrac{az-cx}{y}=\dfrac{bx-ay}{z}\) chứng minh rằng :\(\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}\)
Biết rằng \(\dfrac{bz-xy}{a}\)=\(\dfrac{cx-az}{b}\)=\(\dfrac{ay-bx}{c}\)
CMR: x:y:z=a:b:c
Cho (bz-cy/a)=(cx-az/b)=(ay-bx/c)( a, b, c, x, y, z khác 0). CMR a/x=b/y=c/z
cho bz-cy/a = cx-az/b = ay-bx/c ( x,y , z khác 0 )
cmr : a/x = b/y = c/z
Biết bz-cy/a =cx-az/b =ay-bx/c (a,b,c khác 0)
CMR: x/a=y/b=z/c
Cho bx-ay/c=az-cx/b=cy-bz/a. CMR x/a=y/b=z/c