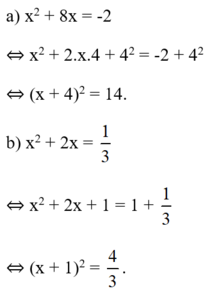
Kiến thức áp dụng
+ Các hằng đẳng thức:
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2.
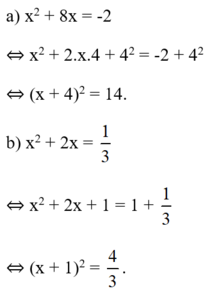
Kiến thức áp dụng
+ Các hằng đẳng thức:
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2.
Cho các phương trình: x 2 + 8 x = - 2
Hãy cộng vào hai vế của mỗi phương trình cùng một số thích hợp để được một phương trình mà vế trái thành một bình phương.
Cho các phương trình: x 2 + 2 x = 1 3
Hãy cộng vào hai vế của mỗi phương trình cùng một số thích hợp để được một phương trình mà vế trái thành một bình phương.
Giải các phương trình sau bằng cách biến đổi chúng thành những phương trình với vế trái là một bình phương còn vế phải là một hằng số: 3 x 2 + 2 3 x - 2 = 0
Giải các phương trình sau bằng cách biến đổi chúng thành những phương trình với vế trái là một bình phương còn vế phải là một hằng số: x 2 + 2 x - 1 = 0
Giải các phương trình sau bằng cách biến đổi chúng thành những phương trình với vế trái là một bình phương còn vế phải là một hằng số. 3 x 2 – 12x + 1 = 0
Người ta viết lên bảng phương trình:
(x−1)(x−2)(x−3)...(x−2016)=(x−1)(x−2)(x−3)...(x−2016)
với 2016 nhân tử bậc nhất ở mỗi vế. Hãy tìm số nguyên dương k nhỏ nhất để có thể xóa đi k nhân tử trong số 4032 nhân tử nêu trên sao cho mỗi vế còn ít nhất một nhân tử và phương trình thu được không có nghiệm thực.
Giải các phương trình sau bằng cách biến đổi chúng thành những phương trình với vế trái là một bình phương còn vế phải là một hằng số: x 2 - 3x + 1 = 0
Giải các phương trình sau bằng cách biến đổi chúng thành những phương trình với vế trái là một bình phương còn vế phải là một hằng số. 3 x 2 – 6x + 5 = 0
Giải các phương trình sau bằng cách biến đổi chúng thành những phương trình với vế trái là một bình phương còn vế phải là một hằng số: 5 x 2 - 7x + 1 = 0