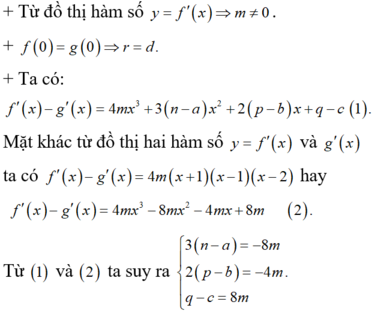Các câu hỏi tương tự
Cho hàm số yf(x) có đạo hàm liên tục trên R và có đồ thị hàm số yf (x) như hình vẽ bên. Xét hàm số g(x)f(x^2-3) và các mệnh đề sau:1. Hàm số g(x) có 3 điểm cực trị.2. Hàm số g(x)đạt cực tiểu tại x 0.3. Hàm số g(x)đạt cực đại tại x 2.4. Hàm số g(x)đồng biến trên khoảng (-2;0).5. Hàm số g(x)nghịch biến trên khoảng (-1;1). Có bao nhiêu mệnh đề đúng trong các mệnh đề trên? A. 1. B. 4. C. 3. D. 2.
Đọc tiếp
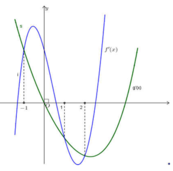
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
Cho hàm số bậc 3:yf(x) có đồ thị như hình vẽ.Xét hàm số g(x)f[(x)]. Trong các mệnh đề dưới đây:g(x) đồng biến trên (-∞;0) và (2;+∞).Hàm số g(x) có bốn điểm cực trị.
m
a
x
-
1
;
1
g
x
0
.Phương trình g(x)0 có ba nghiệm.Số mệnh đề đúng là A. 3. B. 2. C. 1. D. 4.
Đọc tiếp
Cho hàm số bậc 3:y=f(x) có đồ thị như hình vẽ.
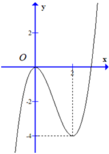
Xét hàm số g(x)=f[(x)]. Trong các mệnh đề dưới đây:
g(x) đồng biến trên (-∞;0) và (2;+∞).
Hàm số g(x) có bốn điểm cực trị.
m a x - 1 ; 1 g x = 0 .
Phương trình g(x)=0 có ba nghiệm.
Số mệnh đề đúng là
A. 3.
B. 2.
C. 1.
D. 4.
Cho hàm số y f(x) có đạo hàm liên tục trên R đồ thị hàm số y f’(x) như hình vẽ.Biết f(2) –6, f(–4) –10 và hàm số g(x) f(x)+
x
2
2
, g(x) có ba điểm cực trị. Phương trình g(x) 0? A. Có đúng 2 nghiệm B. Vô nghiệm C. Có đúng 3 nghiệm D. Có đúng 4 nghiệm
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên R đồ thị hàm số y = f’(x) như hình vẽ.
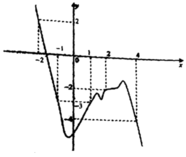
Biết f(2) = –6, f(–4) = –10 và hàm số g(x) = f(x)+ x 2 2 , g(x) có ba điểm cực trị.
Phương trình g(x) = 0?
A. Có đúng 2 nghiệm
B. Vô nghiệm
C. Có đúng 3 nghiệm
D. Có đúng 4 nghiệm
Cho hàm số
f
(
x
)
a
x
2
+
2
b
x
3
-
3
c
x
2
-
4
d
x
+
5
h
(a,b,c,d,hÎZ). Hàm số yf’(x) có đồ thị như hình vẽ bên. Tập nghiệm thực của phương trình f(x)5h có số phần tử bằng A. 3 B. 4 C. 2 D. 1
Đọc tiếp
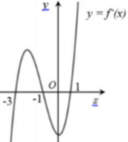
Cho hàm số f ( x ) = a x 2 + 2 b x 3 - 3 c x 2 - 4 d x + 5 h (a,b,c,d,hÎZ). Hàm số y=f’(x) có đồ thị như hình vẽ bên. Tập nghiệm thực của phương trình f(x)=5h có số phần tử bằng
A. 3
B. 4
C. 2
D. 1
Cho hai hàm số yf(x) và yg(x) là các hàm xác định và liên tục trên R và có đồ thị như hình vẽ bên (trong đó đường cong đậm hơn là của đồ thị hàm số yf(x). Có bao nhiêu số nguyên m để phương trình f(1-g(2x-1))m có nghiệm thuộc đoạn
-
1
;
5
2
A. 8 B. 3 C. 6 D. 4
Đọc tiếp
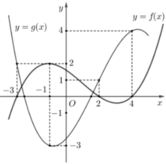
Cho hai hàm số y=f(x) và y=g(x) là các hàm xác định và liên tục trên R và có đồ thị như hình vẽ bên (trong đó đường cong đậm hơn là của đồ thị hàm số y=f(x). Có bao nhiêu số nguyên m để phương trình f(1-g(2x-1))=m có nghiệm thuộc đoạn - 1 ; 5 2
A. 8
B. 3
C. 6
D. 4
Cho hai hàm số
f
(
x
)
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
với
a
≠
0
và g(x)
p
x
2
+
q
x
-
3
c
ó
đồ thị như...
Đọc tiếp
Cho hai hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e với a ≠ 0 và g(x)= p x 2 + q x - 3 c ó đồ thị như hình vẽ bên dưới. Đồ thị hàm số y=f(x) đi qua gốc tọa độ và cắt đồ thị hàm số y=g(x) tại bốn điểm có hoành độ lần lượt là -2;-1;1 và m. Tiếp tuyến của đồ thị hàm số y=f(x)-g(x) tại điểm có hoành độ x=-2 có hệ số góc bằng -15/2. Gọi (H) là hình phẳng giới hạn bởi đồ thị hai hàm số y=f(x) và y=g(x) (phần được tô đậm trong hình vẽ). Diện tích của hình (H) bằng

A. 1553 120
B. 1553 240
C. 1553 60
D. 1553 30
Cho hàm số
f
x
m
x
4
+
n
x
3
+
p
x
2
+
q
x
+
r
(
m
,
n
,
p
,
q
,
r
∈
R
)
. Hàm số yf(x) có đồ thị như hình vẽ bên. Tập nghiệm của phương trình f(x)r có số phần tử là A....
Đọc tiếp
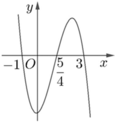
Cho hàm số f x = m x 4 + n x 3 + p x 2 + q x + r ( m , n , p , q , r ∈ R ) . Hàm số y=f'(x) có đồ thị như hình vẽ bên. Tập nghiệm của phương trình f(x)=r có số phần tử là
A. 4
B. 3
C. 1
D. 2
Cho hàm số
f
x
m
x
4
+
n
x
3
+
p
x
2
+
q
x
+
r
m
,
n
,
p
,
q
,
r
...
Đọc tiếp
Cho hàm số f x = m x 4 + n x 3 + p x 2 + q x + r m , n , p , q , r ∈ ℝ . Hàm số y = f¢(x) có đồ thị như hình vẽ bên.
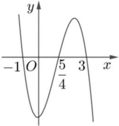
Tập nghiệm của phương trình f (x) = r có số phần tử là
A. 4
B. 3
C. 1
D. 2
Cho các số thực a, b, c, d thỏa mãn 0 a b c d và hàm số y f(x). Biết hàm số y f(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y f(x) trên
[
0
;
d
]
. Khẳng định nào sau đây là khẳng định đúng? A. M + m f(b) + f(a) B. M + m f(d) + f(c) C. M + m f(0) + f(c) D. M + m f(0) + f(a)
Đọc tiếp
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?

A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Cho hàm số yf(x) có đạo hàm trên R thỏa mãn f(-1) f(3) 0 và đồ thị hàm số yf (x) có dạng như hình vẽ. Hàm số y
[
f
(
x
)
]
2
nghịch biến trên khoảng nào trong các khoảng sau? A. (-2;1). B. (1;2). C. (0;4). D. (-2;2).
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên R thỏa mãn f(-1)= f(3)= 0 và đồ thị hàm số y=f' (x) có dạng như hình vẽ. Hàm số y= [ f ( x ) ] 2 nghịch biến trên khoảng nào trong các khoảng sau?
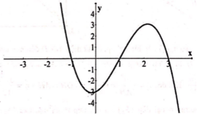
A. (-2;1).
B. (1;2).
C. (0;4).
D. (-2;2).