Các câu hỏi tương tự
Cho dãy số
u
(
n
)
xác định bởi
u
(
1
)
1
;
u
(
m
+
n
)
u...
Đọc tiếp
Cho dãy số u ( n ) xác định bởi u ( 1 ) = 1 ; u ( m + n ) = u ( m ) + u ( n ) + m n , ∀ m , n ∈ ℕ * . Tính u ( 2017 )
A. 2035153
B. 2035154
C. 2035155
D. 2035156
Cho dãy số (U n) với U n = 2n/ n^2 + 1 , ∀ n ∈ N*
a) Viết 5 số hạng đầu
b) số 9/U¹ là hạng thứ mấy
c) chứng minh dãy số bị giảm và bị chặn
Xem chi tiết
Cho dãy số (U n) với U n = 2n/ n^2 + 1 , ∀ n ∈ N*
a) Viết 5 số hạng đầu
b) số 9/U¹ là hạng thứ mấy
c) chứng minh dãy số bị giảm và bị chặn
Xem chi tiết
Cho
(
a
,
b
∈
N
*
,
(
a
,
b
)
1
;
n
∈
a
b
+
1
,
a
b
+
2
. Kí hiệu
r...
Đọc tiếp
Cho ( a , b ∈ N * , ( a , b ) = 1 ; n ∈ a b + 1 , a b + 2 .
Kí hiệu r n là số cặp số ( u , v ) ∈ N * × N *
sao cho n = a u + b v . Tìm lim n → ∞ r n n = 1 a b .
![]()
![]()
![]()
![]()
một xạ thủ bắn 2 viên vào bia.Xác suất để viên I,II bắn trượt là 0,4;0,3. Tính xác suất các biến cố a)M"có ít nhất 1 viên trúng" b)N"1 viên trúng 1 viên trượt"
Bài 2. (1 điểm) Trong hình sau, khi được kéo ra khơi vị trí cân bằng ờ điểm $O$ và buông tay, lực đàn hồi của lò xo khiến vật $A$ gắn ở đầu của lò xo dao động quanh $O$.
Tọa độ $s$ cm của $A$ trên trục $Ox$ vào thời điểm $t$ (giây) sau khi buông tay được xác định bởi công thức $s10 sin left(10 t+dfrac{pi}{2}right)$. Vào các thời điểm nào thì $s-5 sqrt{3} $ cm?
Đọc tiếp
Bài 2. (1 điểm) Trong hình sau, khi được kéo ra khơi vị trí cân bằng ờ điểm $O$ và buông tay, lực đàn hồi của lò xo khiến vật $A$ gắn ở đầu của lò xo dao động quanh $O$.
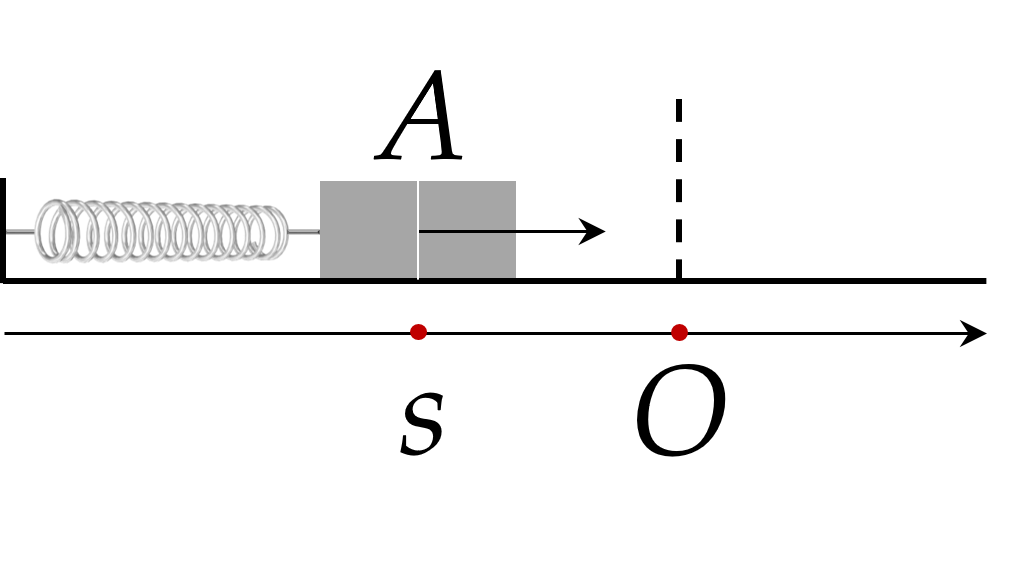
Tọa độ $s$ cm của $A$ trên trục $Ox$ vào thời điểm $t$ (giây) sau khi buông tay được xác định bởi công thức $s=10 \sin \left(10 t+\dfrac{\pi}{2}\right)$. Vào các thời điểm nào thì $s=-5 \sqrt{3} $ cm?
cho dãy số (un):\(\left\{{}\begin{matrix}u_1=2010\\u^2+2019u_n-2011u_{n+1}+1=0\end{matrix}\right.\)
tìm lim\(\left(\Sigma^n_{i=1}\dfrac{1}{u_i+2010}\right)\)
MỌI NGƯỜI GIÚP MÌNH MÔN TIN VỚI Ạ!Cho dãy số (a1, a2, a3, ..., an) là một hoán vị bất kỳ của tập hợp (1, 2, 3, ..., n). Dãy số (b1, b2, b3, ..., bn) gọi là nghịch thế của dãy a nếu bi là số phần tử đứng trước số i trong dãy a mà lớn hơn i.Ví dụ:Dãy a là: 3 2 5 7 1 4 6Dãy b là: 4 1 0 2 0 1 0a. Cho dãy a, hãy xây dựng chương trình tìm dãy b.b. Cho dãy b, xây dựng chương trình tìm dãy a.Dữ liệu vào: Trong file NGICH.INP với nội dung:-Dòng đầu tiên là số n (1 n 10 000).-Các dòng tiếp theo là n số...
Đọc tiếp
MỌI NGƯỜI GIÚP MÌNH MÔN TIN VỚI Ạ!
Cho dãy số (a1, a2, a3, ..., an) là một hoán vị bất kỳ của tập hợp (1, 2, 3, ..., n). Dãy số (b1, b2, b3, ..., bn) gọi là nghịch thế của dãy a nếu bi là số phần tử đứng trước số i trong dãy a mà lớn hơn i.
Ví dụ:
Dãy a là: 3 2 5 7 1 4 6
Dãy b là: 4 1 0 2 0 1 0
a. Cho dãy a, hãy xây dựng chương trình tìm dãy b.
b. Cho dãy b, xây dựng chương trình tìm dãy a.
Dữ liệu vào: Trong file NGICH.INP với nội dung:
-Dòng đầu tiên là số n (1 <= n <= 10 000).
-Các dòng tiếp theo là n số của dãy a, mỗi số cách nhau một dấu cách,
-Các dòng tiếp theo là n số của dãy b, mỗi số cách nhau bởi một dấu cách.
Dữ liệu ra: Trong file NGHICH.OUT với nội dung:
-N số đầu tiên là kết quả của câu a
-Tiếp đó là một dòng trống và sau đó là n số kết quả của câu b (nếu tìm được dãy a).
cho đồ thị n cạnh và v đỉnh. đồ thị này liên thông và các đồ thị con đơn của nó rời nhau nếu có.
c/m n bé hơn hoặc bằng n/3+n-1
Trong các chữ I, J , H, L, P , M, N. Có bao nhiêu chữ có 2 trụcđối xứng
A.1
B.2
C.3
D.4










