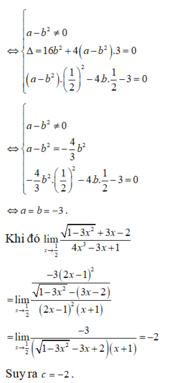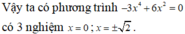Các câu hỏi tương tự
Chứng minh rằng các phương trình sau luôn có nghiệm: a)x^5 - 3x+3=0 b)x^5+x-1=0 c)x^4+x^3-3x^2+x+1=0
Cho phương trình 3x2-c=a(x2-2x+1)-b(x-1) tìm 3 số nguyên a,b,c để phương trình có nghiệm với mọi x thược R.
Bài 1: Phương trình căn 2 cot x + căn 2=0 có tổng các nghiệm khi k =0 và k=1?
A.3pi/4 B.5pi/4 C.4pi/3 D.pi/2Bài 2:cho sin a=1/3,0<a<pi/2 tính sin( a-pi/4) Bài 3:cho cos a=-2/3,pi/2<a<pi tính cos ( a+pi/3)
Giúp vs bạn
Cho đa thức f(x) = x^2+ax+b; a, b ∈ R. Giả sử phương trình f (f(x)) = 0 có 4 nghiệm thực phân biệt và tổng của hai trong bốn nghiệm đó bằng −1. Chứng minh rằng b ≤ − 1/4
9 tháng 5 2021 lúc 20:39
Cho 1/3(m-1)x³-(m-1)x²+(m-3)x+2. Tìm m để a)y'=0 có 2 nghiệm phân biệt cùng dương b)y'=0 có 2 nghiệm phân biệt trái dấu c)y'=0 có 2 nghiệm phân biệt|x1-x2|= căn 2 d)y' lớn hơn hoặc bằng 0 với mọi x e)y' nhỏ hơn hoặc bằng 0 với mọi x
10 tháng 5 2021 lúc 19:25
Cho 1/3(m-1)x³-(m-1)x²+(m-3)x+2. Tìm m để a)y'=0 có 2 nghiệm phân biệt cùng dương b)y'=0 có 2 nghiệm phân biệt trái dấu c)y'=0 có 2 nghiệm phân biệt|x1-x2|= căn 2 d)y' lớn hơn hoặc bằng 0 với mọi x e)y' nhỏ hơn hoặc bằng 0 với mọi x
Cho biết : \(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{ax^2+1}-bx-2}{x^3-3x+2}\left(a,b\in R\right)\) có kết quả là một số thực. Giá trị của biểu thức \(a^2+b^2\) ?
Câu 1: Tính giới hạn a, limdfrac{2-5^{n-2}}{3^n2.5^n} b,limdfrac{2-5^{n+2}}{3^n-2.5^n}Câu 2 :CMR :x^4+x^3-3x^2+x+10 có ít nhất một nghiệm âm lớn hơn -1Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
Đọc tiếp
Câu 1: Tính giới hạn
a, lim\(\dfrac{2-5^{n-2}}{3^n=2.5^n}\) b,lim\(\dfrac{2-5^{n+2}}{3^n-2.5^n}\)
Câu 2 :CMR :\(x^4+x^3-3x^2+x+1=0\) có ít nhất một nghiệm âm lớn hơn -1
Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
9 tháng 5 2021 lúc 20:47
Cho f(x)=1/3(m-1)x³-mx²+(m+2)x-5. Tìm m để a)f'(x) lớn hơn hoặc bằng 0 với mọi x b)f'(x) nhỏ hơn hoặc bằng 0 với mọi x c)f'(x)=0 có 2 nghiệm cùng âm d)f'(x)=0 có nghiệm thỏa mãn x1+2x2=1