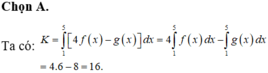Các câu hỏi tương tự
Cho đa thức K (x) = a+b (x - 1) + c (x - 1). (x - 2)
Tìm a; b; c biết K (1) = 1, K (2) =2; K (0) = 5
Cho hàm số
f
(
x
)
a
x
+
b
c
x
+
d
với a,b,c,d là các số thực và c
≠
0. Biết f(1)1, f(2)2 và f(f(x))x với mọi
x
≠
-
d
c
. Tính
l
i
m...
Đọc tiếp
Cho hàm số f ( x ) = a x + b c x + d với a,b,c,d là các số thực và c ≠ 0. Biết f(1)=1, f(2)=2 và f(f(x))=x với mọi x ≠ - d c . Tính l i m x → ∞ f ( x ) .
A. 3 2
B. 5 6
C. 2 3
D. 6 5
bài 3: tính nhanh:a) -5 phần 9 + 3 phần 5 - 3 phần 9 + -2 phần 5b) 5 phần 17 - 9 phần 15 - 2 phần 17 + -2 phần 5c) ( 1 phần 9 - 9 phần 17 ) + 3 phần 6 - ( 12 phần 17 - 1 phần 2 ) + 5 phần 9bài 4: tìm xa) 3 phần 4 - x 1b) x + 4 1 phần 5c) x phần 4 - 3 phần 7 + 2 phần 5 31 phần 140Toán 6 ! giúp mình đi mình tick cho các bạn! d) 5 phần 12 + 5 phần x - 1 phần 8 1 phần 2
Đọc tiếp
bài 3: tính nhanh:
a) -5 phần 9 + 3 phần 5 - 3 phần 9 + -2 phần 5
b) 5 phần 17 - 9 phần 15 - 2 phần 17 + -2 phần 5
c) ( 1 phần 9 - 9 phần 17 ) + 3 phần 6 - ( 12 phần 17 - 1 phần 2 ) + 5 phần 9
bài 4: tìm x
a) 3 phần 4 - x = 1
b) x + 4 = 1 phần 5
c) x phần 4 - 3 phần 7 + 2 phần 5 = 31 phần 140
Toán 6 ! giúp mình đi mình tick cho các bạn!
d) 5 phần 12 + 5 phần x - 1 phần 8 = 1 phần 2
Cho hai hàm số f(x)và g(x) liên tục trên
K
,
a
,
b
∈
K
. Khẳng định nào sau đây là khẳng định sai? A.
∫
a
b
f
x
+
g
x
d
x
∫...
Đọc tiếp
Cho hai hàm số f(x)và g(x) liên tục trên K , a , b ∈ K . Khẳng định nào sau đây là khẳng định sai?
A. ∫ a b f x + g x d x = ∫ a b f x d x + ∫ a b g x d x .
B. ∫ a b k . f x d x = k ∫ a b f x d x .
C. ∫ a b f x . g x d x = ∫ a b f x d x . ∫ a b g x d x .
D. ∫ a b f x − g x d x = ∫ a b f x d x − ∫ a b g x d x .
Cho hàm số
y
f
x
a
x
3
+
b
x
3
+
c
x
+
d
a
,
b
,
c
,
d
∈
ℝ
;
a
≠...
Đọc tiếp
Cho hàm số y = f x = a x 3 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a ≠ 0 biết f'(-1)=3. Tính lim ∆ x → ∞ f 1 + ∆ x + f 1 ∆ x
A. 3
B. -3
C. 1
D. -1
Biết F(x) là nguyên hàm của f(x) trên R thỏa mãn
∫
1
e
F
(
x
)
d
(
ln
x
)
3
và F(e)5. Tính
∫
1
e
ln
x
.
f
(
x
)
d
x
A. I3 B. I-3 C. I2 D. I-2
Đọc tiếp
Biết F(x) là nguyên hàm của f(x) trên R thỏa mãn ∫ 1 e F ( x ) d ( ln x ) = 3 và F(e)=5. Tính ∫ 1 e ln x . f ( x ) d x
A. I=3
B. I=-3
C. I=2
D. I=-2
Trong các hàm số
f
(
x
)
log
2
x
;
g
(
x
)
−
1
2
x
3
+
1
;
h
x
x
1
3...
Đọc tiếp
Trong các hàm số f ( x ) = log 2 x ; g ( x ) = − 1 2 x 3 + 1 ; h x = x 1 3 ; k ( x ) = 3 x 2 có bao nhiêu hàm số đồng biến trên R?
A. 2
B. 3
C. 4
D. 1
Cho hàm số yf(x) và yg(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị các hàm số yf(x) , yg(x) và hai đường thẳng x a, x b(a b) Diện tích của D được tính theo công thức A.
S
∫
a
b
f
x
-
g
x
d
x
B. ...
Đọc tiếp
Cho hàm số y=f(x) và y=g(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị các hàm số y=f(x) , y=g(x) và hai đường thẳng x= a, x= b(a < b) Diện tích của D được tính theo công thức
A. S = ∫ a b f x - g x d x
B. S = ∫ a b f x - g x d x
C. ∫ a b f x d x - ∫ a b g x d x
D. S = ∫ b a f x - g x d x
Tìm các số x, y, z, t, k, sao cho ta có đẳng thức sau:
\(0,4+x-4\frac{1}{5}-2,7=3,75-x+y-2,25=\)
\(=2,5-3\frac{2}{5}+4,5-14,1=-0,7+z+t-8\frac{4}{5}=\)
\(=-10\frac{3}{4}-1,75-t-k=9,80+k-3,02+z.\)